문제 링크
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
문제
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]
N x M 크기의 행렬 모양의 게임 맵이 있습니다. 이 맵에는 내구도를 가진 건물이 각 칸마다 하나씩 있습니다. 적은 이 건물들을 공격하여 파괴하려고 합니다. 건물은 적의 공격을 받으면 내구도가 감소하고 내구도가 0이하가 되면 파괴됩니다. 반대로, 아군은 회복 스킬을 사용하여 건물들의 내구도를 높이려고 합니다.
적의 공격과 아군의 회복 스킬은 항상 직사각형 모양입니다.
예를 들어, 아래 사진은 크기가 4 x 5인 맵에 내구도가 5인 건물들이 있는 상태입니다.

첫 번째로 적이 맵의 (0,0)부터 (3,4)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.

두 번째로 적이 맵의 (2,0)부터 (2,3)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같이 4개의 건물이 파괴되는 상태가 됩니다.

세 번째로 아군이 맵의 (1,0)부터 (3,1)까지 회복하여 2만큼 건물의 내구도를 높이면 아래와 같이 2개의 건물이 파괴되었다가 복구되고 2개의 건물만 파괴되어있는 상태가 됩니다.

마지막으로 적이 맵의 (0,1)부터 (3,3)까지 공격하여 1만큼 건물의 내구도를 낮추면 아래와 같이 8개의 건물이 더 파괴되어 총 10개의 건물이 파괴된 상태가 됩니다. (내구도가 0 이하가 된 이미 파괴된 건물도, 공격을 받으면 계속해서 내구도가 하락하는 것에 유의해주세요.)

최종적으로 총 10개의 건물이 파괴되지 않았습니다.
건물의 내구도를 나타내는 2차원 정수 배열 board와 적의 공격 혹은 아군의 회복 스킬을 나타내는 2차원 정수 배열 skill이 매개변수로 주어집니다. 적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수를 return하는 solution함수를 완성해 주세요.
제한사항
- 1 ≤ board의 행의 길이 (= N) ≤ 1,000
- 1 ≤ board의 열의 길이 (= M) ≤ 1,000
- 1 ≤ board의 원소 (각 건물의 내구도) ≤ 1,000
- 1 ≤ skill의 행의 길이 ≤ 250,000
- skill의 열의 길이 = 6
- skill의 각 행은 [type, r1, c1, r2, c2, degree]형태를 가지고 있습니다.
- type은 1 혹은 2입니다.
- type이 1일 경우는 적의 공격을 의미합니다. 건물의 내구도를 낮춥니다.
- type이 2일 경우는 아군의 회복 스킬을 의미합니다. 건물의 내구도를 높입니다.
- (r1, c1)부터 (r2, c2)까지 직사각형 모양의 범위 안에 있는 건물의 내구도를 degree 만큼 낮추거나 높인다는 뜻입니다.
- 0 ≤ r1 ≤ r2 < board의 행의 길이
- 0 ≤ c1 ≤ c2 < board의 열의 길이
- 1 ≤ degree ≤ 500
- type이 1이면 degree만큼 건물의 내구도를 낮춥니다.
- type이 2이면 degree만큼 건물의 내구도를 높입니다.
- type은 1 혹은 2입니다.
- 건물은 파괴되었다가 회복 스킬을 받아 내구도가 1이상이 되면 파괴되지 않은 상태가 됩니다. 즉, 최종적으로 건물의 내구도가 1이상이면 파괴되지 않은 건물입니다.
예제 입력 1
4 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
5 5 5 5 5
4
1 0 0 3 4 4
1 2 0 2 3 2
2 1 0 3 1 2
1 0 1 3 3 1예제 출력 1
10예제 입력 2
3 3
1 2 3
4 5 6
7 8 9
3
1 1 1 2 2 4
1 0 0 1 1 2
2 2 0 2 0 100예제 출력 2
6입출력 예 설명
입출력 예 #1
문제 예시와 같습니다.
입출력 예 #2
<초기 맵 상태>

첫 번째로 적이 맵의 (1,1)부터 (2,2)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
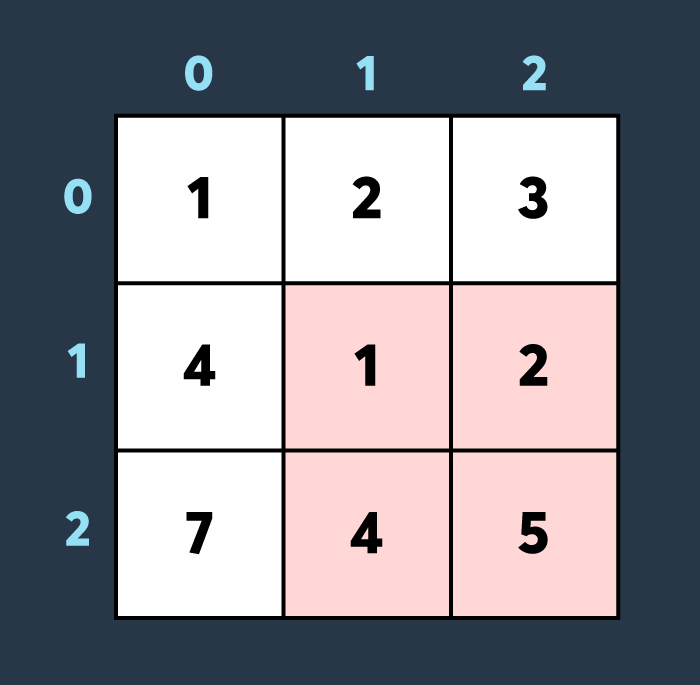
두 번째로 적이 맵의 (0,0)부터 (1,1)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
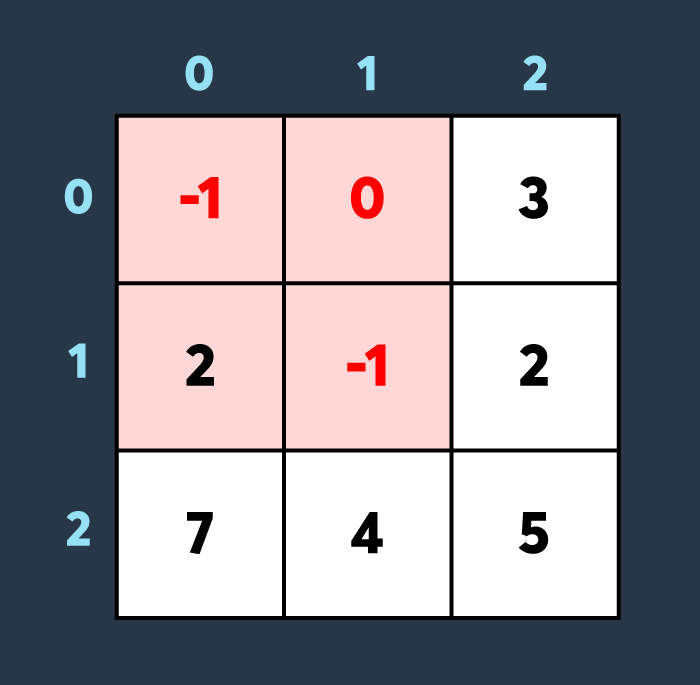
마지막으로 아군이 맵의 (2,0)부터 (2,0)까지 회복하여 100만큼 건물의 내구도를 높이면 아래와 같은 상황이 됩니다.
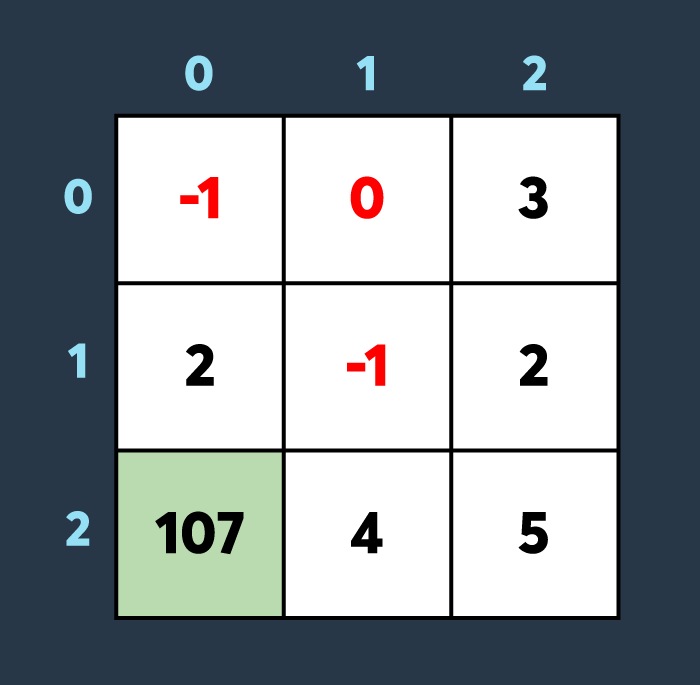
총, 6개의 건물이 파괴되지 않았습니다. 따라서 6을 return 해야 합니다.
알고리즘 분류
- 누적 합
풀이
누적 합을 활용해야 하는데, imos 알고리즘을 이용한다.
2차원 imos에서는 시작 지점이 (r1, c1), 끝 지점이 (r2, c2)면 (r1, c1)에서 늘어나는 수치만큼 더해주고, (r2 + 1, c1), (r1, c2 + 1)에서 늘어나는 수치만큼 감소시켜야 한다.
그러니까 가로, 세로 각각 1차원 imos처럼 시작 부분을 증가시키고 끝 부분을 감소시키는 식이다.
또한 가로의 끝과 세로의 끝이 교차하는 지점에서 다시 늘어나는 수치만큼 더해준다.
2차원 imos 배열을 구했으면 해당 배열로 늘어나는 수치의 누적 합을 구한다.
마지막으로 각 칸마다 현재 내구도 + 누적 합 배열에 기록된 내구도의 변화량이 1 이상인 건물의 개수를 센다.
imos를 떠올리긴 했으나 2차원 imos는 해본 적이 없어서 구글링했다.
해결 완료 시각

코드
import java.util.*;
class Solution {
private static int N, M;
private static int[][] Imos;
private static int[][] Sums;
private static int Answer;
public int solution(int[][] board, int[][] skill) {
N = board.length;
M = board[0].length;
Imos = new int[N + 1][M + 1];
Sums = new int[N + 1][M + 1];
for (int i = 0; i < skill.length; i++) {
int type = skill[i][0];
int r1 = skill[i][1];
int c1 = skill[i][2];
int r2 = skill[i][3] + 1;
int c2 = skill[i][4] + 1;
int degree = skill[i][5];
if (type == 1) {
degree = -degree;
}
Imos[r1][c1] += degree;
Imos[r1][c2] -= degree;
Imos[r2][c1] -= degree;
Imos[r2][c2] += degree;
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
Sums[i][j] = Sums[i - 1][j] + Sums[i][j - 1] - Sums[i - 1][j - 1] + Imos[i - 1][j - 1];
if (board[i - 1][j - 1] + Sums[i][j] >= 1) {
Answer++;
}
}
}
return Answer;
}
}'Programmers > Level 3' 카테고리의 다른 글
| [Programmers/Level 3] 숫자 게임(Java) (0) | 2024.11.14 |
|---|---|
| [Programmers/Level 3] 보석 쇼핑(Java) (1) | 2024.11.14 |
| [Programmers/Level 3] 110 옮기기(Java) (3) | 2024.10.23 |
| [Programmers/Level 3] 미로 탈출 명령어(Java) (0) | 2024.10.23 |
| [Programmers/Level 3] 정수 삼각형(Java) (0) | 2024.10.10 |