문제 링크
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제

당신은 일렬로 나열된 n개의 집에 택배를 배달하려 합니다. 배달할 물건은 모두 크기가 같은 재활용 택배 상자에 담아 배달하며, 배달을 다니면서 빈 재활용 택배 상자들을 수거하려 합니다.
배달할 택배들은 모두 재활용 택배 상자에 담겨서 물류창고에 보관되어 있고, i번째 집은 물류창고에서 거리 i만큼 떨어져 있습니다. 또한 i번째 집은 j번째 집과 거리 j - i만큼 떨어져 있습니다. (1 ≤ i ≤ j ≤ n)
트럭에는 재활용 택배 상자를 최대 cap개 실을 수 있습니다. 트럭은 배달할 재활용 택배 상자들을 실어 물류창고에서 출발해 각 집에 배달하면서, 빈 재활용 택배 상자들을 수거해 물류창고에 내립니다. 각 집마다 배달할 재활용 택배 상자의 개수와 수거할 빈 재활용 택배 상자의 개수를 알고 있을 때, 트럭 하나로 모든 배달과 수거를 마치고 물류창고까지 돌아올 수 있는 최소 이동 거리를 구하려 합니다. 각 집에 배달 및 수거할 때, 원하는 개수만큼 택배를 배달 및 수거할 수 있습니다.
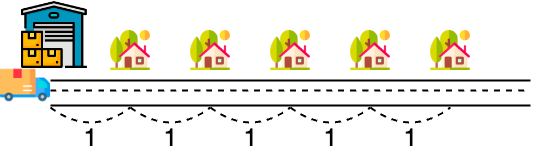
다음은 cap=4 일 때, 최소 거리로 이동하면서 5개의 집에 배달 및 수거하는 과정을 나타낸 예시입니다.
배달 및 수거할 재활용 택배 상자 개수
| 집 #1 | 집 #2 | 집 #3 | 집 #4 | 집 #5 | |
| 배달 | 1개 | 0개 | 3개 | 1개 | 2개 |
| 수거 | 0개 | 3개 | 0개 | 4개 | 0개 |
배달 및 수거 과정
| 집 #1 | 집 #2 | 집 #3 | 집 #4 | 집 #5 | 설명 | |
| 남은 배달/수거 | 1/0 | 0/3 | 3/0 | 1/4 | 2/0 | 물류창고에서 택배 3개를 트럭에 실어 출발합니다. |
| 남은 배달/수거 | 1/0 | 0/3 | 3/0 | 0/4 | 0/0 | 물류창고에서 5번째 집까지 이동하면서(거리 5) 4번째 집에 택배 1개를 배달하고, 5번째 집에 택배 2개를 배달합니다. |
| 남은 배달/수거 | 1/0 | 0/3 | 3/0 | 0/0 | 0/0 | 5번째 집에서 물류창고까지 이동하면서(거리 5) 4번째 집에서 빈 택배 상자 3개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내리고 택배 4개를 트럭에 싣습니다. |
| 남은 배달/수거 | 0/0 | 0/3 | 0/0 | 0/0 | 0/0 | 물류창고에서 3번째 집까지 이동하면서(거리 3) 1번째 집에 택배 1개를 배달하고, 3번째 집에 택배 3개를 배달합니다. |
| 남은 배달/수거 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 3번째 집에서 물류창고까지 이동하면서(거리 3) 2번째 집에서 빈 택배 상자 3개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내립니다. |
16(=5+5+3+3)의 거리를 이동하면서 모든 배달 및 수거를 마쳤습니다. 같은 거리로 모든 배달 및 수거를 마치는 다른 방법이 있지만, 이보다 짧은 거리로 모든 배달 및 수거를 마치는 방법은 없습니다.
트럭에 실을 수 있는 재활용 택배 상자의 최대 개수를 나타내는 정수 cap, 배달할 집의 개수를 나타내는 정수 n, 각 집에 배달할 재활용 택배 상자의 개수를 담은 1차원 정수 배열 deliveries와 각 집에서 수거할 빈 재활용 택배 상자의 개수를 담은 1차원 정수 배열 pickups가 매개변수로 주어집니다. 이때, 트럭 하나로 모든 배달과 수거를 마치고 물류창고까지 돌아올 수 있는 최소 이동 거리를 return 하도록 solution 함수를 완성해 주세요.
제한사항
- 1 ≤ cap ≤ 50
- 1 ≤ n ≤ 100,000
- deliveries의 길이 = pickups의 길이 = n
- deliveries[i]는 i+1번째 집에 배달할 재활용 택배 상자의 개수를 나타냅니다.
- pickups[i]는 i+1번째 집에서 수거할 빈 재활용 택배 상자의 개수를 나타냅니다.
- 0 ≤ deliveries의 원소 ≤ 50
- 0 ≤ pickups의 원소 ≤ 50
- 트럭의 초기 위치는 물류창고입니다.
예제 입력 1
4 5
1 0 3 1 2
0 3 0 4 0예제 출력 1
16예제 입력 2
2 7
1 0 2 0 1 0 2
0 2 0 1 0 2 0예제 출력 2
30
입출력 예 설명
입출력 예 #1
- 문제 예시와 동일합니다.
입출력 예 #2
배달 및 수거할 재활용 택배 상자 개수
| 집 #1 | 집 #2 | 집 #3 | 집 #4 | 집 #5 | 집 #6 | 집 #7 | |
| 배달 | 1개 | 0개 | 2개 | 0개 | 1개 | 0개 | 2개 |
| 수거 | 0개 | 2개 | 0개 | 1개 | 0개 | 2개 | 0개 |
배달 및 수거 과정
| 집 #1 | 집 #2 | 집 #3 | 집 #4 | 집 #5 | 집 #6 | 집 #7 | 설명 | |
| 남은 배달/수거 | 1/0 | 0/2 | 2/0 | 0/1 | 1/0 | 0/2 | 2/0 | 물류창고에서 택배 2개를 트럭에 실어 출발합니다. |
| 남은 배달/수거 | 1/0 | 0/2 | 2/0 | 0/1 | 1/0 | 0/2 | 0/0 | 물류창고에서 7번째 집까지 이동하면서(거리 7) 7번째 집에 택배 2개를 배달합니다. |
| 남은 배달/수거 | 1/0 | 0/2 | 2/0 | 0/1 | 1/0 | 0/0 | 0/0 | 7번째 집에서 물류창고까지 이동하면서(거리 7) 6번째 집에서 빈 택배 상자 2개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내리고 택배 2개를 트럭에 싣습니다. |
| 남은 배달/수거 | 1/0 | 0/2 | 1/0 | 0/1 | 0/0 | 0/0 | 0/0 | 물류창고에서 5번째 집까지 이동하면서(거리 5) 3번째 집에 택배 1개를 배달하고, 5번째 집에 택배 1개를 배달합니다. |
| 남은 배달/수거 | 1/0 | 0/1 | 1/0 | 0/0 | 0/0 | 0/0 | 0/0 | 5번째 집에서 물류창고까지 이동하면서(거리 5) 4번째 집에서 빈 택배 상자 1개를 수거하고 2번째 집에서 빈 택배 상자 1개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내리고 택배 2개를 트럭에 싣습니다. |
| 남은 배달/수거 | 0/0 | 0/1 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 물류창고에서 3번째 집까지 이동하면서(거리 3) 1번째 집에 택배 1개를 배달하고, 3번째 집에 택배 1개를 배달합니다. |
| 남은 배달/수거 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 3번째 집에서 물류창고까지 이동하면서(거리 3) 2번째 집에서 빈 택배 상자 1개를 수거한 후, 수거한 빈 택배 상자를 물류창고에 내립니다. |
30(=7+7+5+5+3+3)의 거리를 이동하면서 모든 배달 및 수거를 마쳤습니다. 같은 거리로 모든 배달 및 수거를 마치는 다른 방법이 있지만, 이보다 짧은 거리로 모든 배달 및 수거를 마치는 방법은 없습니다.
따라서, 30을 return 하면 됩니다.
알고리즘 분류
- 그리디 알고리즘
풀이
일단 정말 문제가 이해가 안 돼서 GPT도 검색해보고 질문하기 쪽에서도 검색해 보고 결국 그냥 이거 보고 했다.
먼저 문제부터 이해를 잘못했는데, 처음에는 배달할 재활용 택배 상자와 빈 택배 상자의 합이 cap개가 넘으면 안 되는 줄 알았는데 그건 아니고 각각 cap개가 넘으면 안 되는 것이었다.
아무튼 그래서 예시를 보니 가장 멀리 떨어져 있는 집부터 탐색하는 것이 좋아보인다고 생각을 하긴 했는데 생각만 하였고 구현 방법은 떠오르지 않아 이곳저곳 검색해보았다.
구현 방법을 정리하자면 다음과 같다.
- 가장 멀리 떨어진 집부터 배달과 수거를 완료하며, 이 때 한 번 이동할 때마다 배달 및 수거하는 택배 상자는 cap개를 초과해서는 안 된다.
- 해당 집에 배달과 수거를 완료했다면, 남아 있는 배달할 수 있는 상자와 수거할 수 있는 상자의 개수를 가지고 그대로 다음 집으로 이동한다.
- 또한 한 번 배달 및 수거를 할 때마다 물류창고랑 해당 집을 왕복해야 하며, 그 때마다 이동 거리에 해당 집까지의 거리 X 2만큼을 누적한다.
문제는 이렇게 해서 구현한다면 시간 초과가 발생하기 때문에 다른 방법을 생각해야 했다. 누적되어 있는 배달할 수 있는 상자의 개수 D와 수거할 수 있는 상자의 개수 P를 계속해서 다음 집으로 가지고 가면서, 현재 집에서 배달해야 하는 상자와 수거해야 하는 상자의 개수를 각각 차감시키고 D와 P가 모두 0 이상의 수가 될 때까지 cap만큼 더하는 것을 반복하면 시간을 단축시킬 수 있을 것이다. 그리고 cap만큼 더한다는 것은 현재 집까지 왕복한다는 것이므로 계속 거리를 누적시킨다.
무조건 cap개까지 더하는 이유는, 현재 집까지 배달 및 수거를 다 완료한 경우, 남아 있는 배달 및 수거가 가능한 횟수를 가지고 그 다음 집으로 이동해서 남아있는 횟수를 전부 소모함으로써 이동할 거리를 줄일 수 있기 때문이다.
해결 완료 시각

코드
- 통과
import java.util.*;
class Solution {
private static int D, P;
private static long Answer;
public long solution(int cap, int n, int[] deliveries, int[] pickups) {
for (int i = (n - 1); i >= 0; i--) {
D -= deliveries[i];
P -= pickups[i];
while (true) {
if ((D >= 0) && (P >= 0)) {
break;
}
D += cap;
P += cap;
Answer += (i + 1) * 2;
}
}
return Answer;
}
}
- 시간 초과
import java.util.*;
class Solution {
private static int D, P;
private static long Answer;
public long solution(int cap, int n, int[] deliveries, int[] pickups) {
for (int i = (n - 1); i >= 0; i--) {
while (true) {
if ((deliveries[i] == 0) && (pickups[i] == 0)) {
break;
}
D = 0;
P = 0;
for (int j = i; j >= 0; j--) {
if (deliveries[j] > 0) {
int nowDelivery = Math.min(cap - D, deliveries[j]);
deliveries[j] -= nowDelivery;
D += nowDelivery;
}
if (pickups[j] > 0) {
int nowPickup = Math.min(cap - P, pickups[j]);
pickups[j] -= nowPickup;
P += nowPickup;
}
if ((D >= cap) && (P >= cap)) {
break;
}
}
Answer += ((i + 1) * 2);
}
}
return Answer;
}
}'Programmers > Level 1~2' 카테고리의 다른 글
| [Programmers/Level 2] 쿼드압축 후 개수 세기(Java) (1) | 2024.10.23 |
|---|---|
| [Programmers/Level 1] 개인정보 수집 유효기간(Java) (2) | 2024.10.23 |
| [Programmers/Level 2] 구명보트(Java) (0) | 2024.10.15 |
| [Programmers/Level 2] 귤 고르기(Java) (1) | 2024.10.10 |
| [Programmers/Level 1] 예산(Java) (0) | 2024.10.10 |