문제 링크
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제
1와 0로 채워진 표(board)가 있습니다. 표 1칸은 1 x 1 의 정사각형으로 이루어져 있습니다. 표에서 1로 이루어진 가장 큰 정사각형을 찾아 넓이를 return 하는 solution 함수를 완성해 주세요. (단, 정사각형이란 축에 평행한 정사각형을 말합니다.)
예를 들어

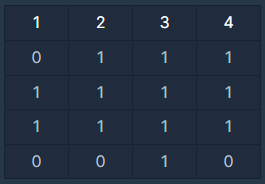
가 있다면 가장 큰 정사각형은

가 되며 넓이는 9가 되므로 9를 반환해 주면 됩니다.
제한사항
- 표(board)는 2차원 배열로 주어집니다.
- 표(board)의 행(row)의 크기 : 1,000 이하의 자연수
- 표(board)의 열(column)의 크기 : 1,000 이하의 자연수
- 표(board)의 값은 1또는 0으로만 이루어져 있습니다.
예제 입력 1
4 4
0 1 1 1
1 1 1 1
1 1 1 1
0 0 1 0예제 출력 1
9예제 입력 2
2 4
0 0 1 1
1 1 1 1예제 출력 2
4
알고리즘 분류
- 다이나믹 프로그래밍
풀이
dp[N][M]에는 현재 칸까지 도달했을 때 정사각형의 한 변의 최솟값을 기록한다.
그러기 위해서는, 현재 칸(board[i][j])이 1이어야 한다.
dp[i][j]은 dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1] 중 최솟값 + 1이 된다.
해결 완료 시각

코드
더보기
import java.util.*;
class Solution {
private static int N, M;
private static int[][] dp;
private static int Answer;
public int solution(int [][]board) {
N = board.length;
M = board[0].length;
dp = new int[N + 1][M + 1];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
dp[i][j] = board[i - 1][j - 1];
}
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
if (dp[i][j] > 0) {
int min = Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]);
dp[i][j] = min + 1;
Answer = Math.max(Answer, min + 1);
}
}
}
return Answer * Answer;
}
}'Programmers > Level 1~2' 카테고리의 다른 글
| [Programmers/Level 2] 귤 고르기(Java) (1) | 2024.10.10 |
|---|---|
| [Programmers/Level 1] 예산(Java) (0) | 2024.10.10 |
| [Programmers/Level 2] 땅따먹기(Java) (2) | 2024.10.10 |
| [Programmers/Level 2] 2 X n 타일링(Java) (0) | 2024.10.10 |
| [Programmers/Level 2] 피보나치 수(Java) (0) | 2024.10.10 |