문제 링크
https://www.acmicpc.net/problem/26260
문제
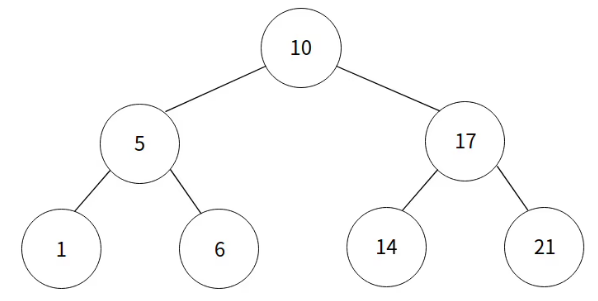
김소마는 최근에 포화 이진 트리에 대해 배웠다. 포화 이진 트리란, 이진 트리에서 리프 노드를 제외한 모든 노드가 두 자식 노드를 가지며, 모든 리프 노드가 채워진 것을 말한다. 아래의 그림을 통해 쉽게 이해하자.

김소마는 예쁜 포화 이진 검색 트리를 그려 만족했지만, 밥 먹다 흘린 소스가 리프 노드 한 개를 가려버렸다. 여기서 이진 검색 트리란, 모든 왼쪽 자식이 자신보다 작고, 모든 오른쪽 자식이 자신보다 큰 이진 트리를 이야기한다.

그림을 버리려던 찰나, 김소마는 갑자기 포화 이진 검색 트리를 유지하며, 임의의 수를 넣을 때, 트리 구조가 어떻게 바뀔지 궁금해졌다. 멍청한 김소마를 위해 당신이 도와주자.
입력
첫 번째 줄에 가려진 노드를 포함한 노드의 개수 N이 주어진다. (N = 2^k−1; 2 ≤ k ≤ 17; k는 정수)
두 번째 줄에 A1, A2, ⋯, AN이 공백으로 구분되어 주어진다. Ai는 i번 노드에 적혀있는 수이다. (0 ≤ Ai ≤ 10^9; 가려진 하나의 노드에 대해서만 Ai = −1) i ≠ j이면 Ai ≠ Aj이다. 노드 번호는 루트 노드부터 시작하여, 같은 깊이 내 왼쪽에서 오른쪽으로 갈수록 증가하는 순서로 매겨진다 (아래 그림 참조).
세 번째 줄에 트리에 넣을 수 X가 주어진다. (0 ≤ X ≤ 10^9; X ≠ Ai)
입력으로 주어지는 모든 수는 정수이다.

출력
첫 번째 줄에 바뀐 트리를 후위(postorder) 순회한 결과를 출력한다. (단, 왼쪽 자식 노드를 먼저 방문한다.)
예제 입력 1
7
10 5 17 1 -1 14 21
18예제 출력 1
1 10 5 17 21 18 14
알고리즘 분류
- 자료 구조
- 그래프 탐색
풀이
주어진 값은 순서대로 주어진 노드들이다. 그러니까 i번째 노드의 자식이 i * 2, i * 2 + 1번째 노드인 것이다.
i번째 노드의 값이 주어져 있지 않다면(= -1), 부모 노드인 i / 2번째 노드를 토대로 임의의 값을 구한다.
예시에서는 5번째 노드의 값이 비어 있다. 따라서, 부모 노드는 2번째 노드이고, 이 노드를 토대로 임의의 값을 결정한다.
2번째 노드의 왼쪽 자식은 4번째 노드이고, 오른쪽 자식은 5번째 노드이다. 따라서 5번째 노드는 2번째 노드보다는 값이 커야 한다.
2번째 노드의 값+1을 5번째 노드의 값으로 한다. 왜냐하면, 현재 포화 이진 검색 트리가 주어졌기 때문에, 사라진 노드 값의 ±1은 나올 수는 없기 때문이다.
사라진 노드의 값을 임의로 복구했으면, 포화 이진 검색 트리를 만든다.
그리고 나서 사라진 노드를 삭제한다.
이번엔 새로 주어진 X를 값으로 가지는 노드를 추가하고, 이진 검색 트리를 재구성한다.
마지막으로 후위 표기법으로 이진 검색 트리의 모든 노드의 값을 출력한다.
코드
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#define MAX 500001
#define FASTIO cin.tie(NULL); cout.tie(NULL); ios::sync_with_stdio(false);
using namespace std;
struct NODE {
int Value;
NODE* Left;
NODE* Right;
NODE(int Value) : Value(Value), Left(nullptr), Right(nullptr) {}
};
int N, X, D;
NODE* Root = nullptr;
vector<int> Vec;
int Answer;
NODE* insert_Node(NODE* Node, int Value) {
if (Node == nullptr) {
return new NODE(Value);
}
if (Value < Node->Value) {
Node->Left = insert_Node(Node->Left, Value);
}
else if (Value > Node->Value) {
Node->Right = insert_Node(Node->Right, Value);
}
return Node;
}
NODE* find_Min(NODE* Node) {
while (Node->Left != nullptr) {
Node = Node->Left;
}
return Node;
}
NODE* find_Max(NODE* Node) {
while (Node->Right != nullptr) {
Node = Node->Right;
}
return Node;
}
NODE* delete_Node(NODE* Node, int Value) {
if (Node == nullptr) {
return Node;
}
if (Value < Node->Value) {
Node->Left = delete_Node(Node->Left, Value);
}
else if (Value > Node->Value) {
Node->Right = delete_Node(Node->Right, Value);
}
else {
if (Node->Left == nullptr) {
NODE* Temp = Node->Left;
delete Node;
return Temp;
}
else if (Node->Right == nullptr) {
NODE* Temp = Node->Right;
delete Node;
return Temp;
}
NODE* Temp = find_Min(Node->Right);
Node->Value = Temp->Value;
Node->Right = delete_Node(Node->Right, Temp->Value);
}
return Node;
}
void postorder(NODE* Node) {
if (Node == nullptr) return;
postorder(Node->Left);
postorder(Node->Right);
cout << Node->Value << " ";
}
void collectValues(NODE* Node, vector<int>& Values) {
if (Node == nullptr) return;
collectValues(Node->Left, Values);
collectValues(Node->Right, Values);
Values.push_back(Node->Value);
}
NODE* constructTree(vector<int>& Values, int Start, int End) {
if (Start > End) {
return nullptr;
}
int Mid = (Start + End) / 2;
NODE* Node = new NODE(Values[Mid]);
Node->Left = constructTree(Values, Start, Mid - 1);
Node->Right = constructTree(Values, Mid + 1, End);
return Node;
}
NODE* getBSTree(NODE* Node) {
vector<int> Values;
collectValues(Node, Values);
sort(Values.begin(), Values.end());
return constructTree(Values, 0, N - 1);
}
void input() {
cin >> N;
for (int i = 0; i < N; i++) {
cin >> X;
Vec.push_back(X);
}
cin >> X;
}
void settings() {
for (int i = 0; i < N; i++) {
if (Vec[i] == -1) {
if (i == 0) {
Vec[i] = Vec[i + 1] + 1;
}
else {
int Index = i + 1;
if (Index % 2 == 0) {
Vec[i] = Vec[(Index / 2) - 1] - 1;
}
else {
Vec[i] = Vec[(Index / 2) - 1] + 1;
}
}
D = Vec[i];
}
int Now = Vec[i];
Root = insert_Node(Root, Now);
}
Root = delete_Node(Root, D);
Root = insert_Node(Root, X);
Root = getBSTree(Root);
}
void print_Answer() {
postorder(Root);
cout << "\n";
}
int main() {
FASTIO
input();
settings();
print_Answer();
return 0;
}'BOJ > Gold' 카테고리의 다른 글
| [BOJ/Gold 3] 백준 1941 소문난 칠공주(Java) (1) | 2024.11.14 |
|---|---|
| [BOJ/Gold 3] 백준 26607 시로코와 은행털기(C++) (2) | 2024.11.01 |
| [BOJ/Gold 4] 백준 2987 사과나무(C++) (1) | 2024.10.29 |
| [BOJ/Gold 4] 백준 20956 아이스크림 도둑 지호(C++) (1) | 2024.10.24 |
| [BOJ/Gold 4] 백준 1715 카드 정렬하기(Java) (0) | 2024.10.15 |