3025번: 돌 던지기
이 모든 사건의 시작은 2주 전이었다. 그 날 상근이는 복도에 누워서 잠을 자고 있었다. 커다란 돌을 들고 그 옆을 지나가던 민혁이는 복도에서 잠을 자는 사람을 처음봐서 신기하게 쳐다보고 있
www.acmicpc.net
문제
이 모든 사건의 시작은 2주 전이었다. 그 날 상근이는 복도에 누워서 잠을 자고 있었다. 커다란 돌을 들고 그 옆을 지나가던 민혁이는 복도에서 잠을 자는 사람을 처음봐서 신기하게 쳐다보고 있었다. 그 때였다. 들고 있던 돌을 상근이의 왼 발에 떨어뜨렸다. 상근이는 응급실로 실려갔고, 한 달 동안 침대에 누워서 휴식을 취해야 한다는 진단을 받았다. 민혁이는 미안한 마음에 하던 일을 모두 중단하고 상근이를 간호하기로 했다.
상근이는 2주 동안 온라인 저지 문제를 풀었다. 2주 동안 문제를 풀다보니 게임을 하고 싶어졌고, 마침 민혁이를 이용해서 게임을 하기로 했다.
상근이의 게임은 R×C 보드를 세워놓은 상태에서 진행한다. 맨 처음에 각 정사각형 칸은 비어있거나 벽으로 막혀있다. 상근이는 민혁이에게 돌을 떨어놓을 열을 지시하고, 민혁이는 가장 윗 행의 그 열에 돌을 놓는다. 돌을 놓은 이후에는 중력에 의해서 돌이 떨어지게 된다.
돌에 작용하는 중력은 다음과 같다.
- 돌의 아랫칸이 벽으로 막혀있거나 가장 아랫줄이라면, 돌은 그 자리에 그대로 멈춰 있는다.
- 돌의 아랫칸이 비어있다면, 돌은 아랫칸으로 이동한다.
- 돌의 아랫칸에 돌이 있다면, 돌은 다음과 같이 미끄러진다.
- 만약 돌의 왼쪽 칸과 왼쪽-아래 칸이 비어있다면, 돌은 왼쪽으로 미끄러진다.
- 만약 돌이 왼쪽으로 미끄러지지 않았고, 오른쪽 칸과 오른쪽-아래 칸이 비어있다면, 돌은 오른쪽으로 미끄러진다.
- 위의 두 경우가 아니라면 돌은 그 자리에 멈추고, 다시는 움직이지 않는다.
민혁이는 돌의 이동이 멈춘 이후에 다른 돌을 던지기 시작한다.
보드의 초기 상태와 민혁이가 돌을 놓은 열의 번호가 순서대로 가 주어졌을 때, 모든 돌을 던진 이후에 보드의 상태를 구하는 프로그램을 작성하시오.
민혁이는 항상 제일 윗 칸이 비어있는 칸에만 돌을 던진다.
입력
첫째 줄에 보드의 크기 R과 C가 주어진다. (1 ≤ R ≤ 30,000, 1 ≤ C ≤ 30)
다음 R개 줄에는 C개의 문자가 주어지며, 보드의 초기 상태이다. '.'는 빈 칸, 'X'는 벽으로 막힌 곳을 나타낸다.
다음 줄에는 돌을 던진 횟수 N이 주어진다. (1 ≤ N ≤ 100,000)
다음 N개 줄에는 돌을 던진 열의 위치가 순서대로 주어진다. (가장 왼쪽 열의 번호는 1번)
출력
총 R개 줄에 걸쳐서 보드의 게임이 모두 끝난 후의 상태를 출력한다. 돌은 'O'로 출력한다.
예제 입력 1
5 4
....
....
X...
....
....
4
1
1
1
1예제 출력 1
....
O...
X...
....
OOO.예제 입력 2
7 6
......
......
...XX.
......
......
.XX...
......
6
1
4
4
6
4
4예제 출력 2
......
...O..
...XX.
......
.OO...
.XX...
O..O.O알고리즘 분류
- 구현
- 시뮬레이션
- 자료 구조
- 재귀
- 다이나믹 프로그래밍
풀이
너무 어려운 나머지 이 형님이 쓰신 글을 참고하였다.
돌의 경로를 직접적으로 찾는 작업을 한다면 시간 초과가 걸릴 것이다.
따라서, 우리는 돌을 던질 때마다 돌들의 경로를 적어 줄 것이다.
예제 1을 보면, 5*4의 보드에 (3, 1) 칸에 벽이 있고, 이 보드에서 돌을 던진다고 되어 있다.
총 4개의 돌을 던지는데, 우선 첫 번째 돌은 1열에서 던진다.

1열에서 던진 돌은 (3, 1)에 존재하는 벽과 만난다. 그런데 돌의 아랫칸이 벽으로 막혀 있다면, 돌은 그 자리에 멈춘다고 하였다.

여기서 열의 어떤 칸에 벽 또는 돌이 있는지를 확인하기 위해서 set을 사용해준다. set은 이진 트리로 구현되어 있으며, 원소의 값의 중복이 허용되지 않는 자료구조이다. 이 set을 이용하여, 돌이 떨어질 높이를 찾아 줄 것이다. 그러기 위해서는, set에 벽과 떨어진 돌의 위치를 삽입하는 것이 필요하다. 즉, set 배열을 열의 개수만큼 선언하고, 해당 열의 set에 열에 존재하는 벽과 돌의 높이를 저장해준다. 그렇다면, 지금 1열의 set에는 오직 3만이 삽입되어 있는 상태라고 할 수 있다.
아무튼 돌이 (2, 1)에 떨어졌기 때문에, 1열의 set에서 3을 지우고 2를 삽입시켜준다.
이제 두번째 돌을 떨어뜨릴 건데, 두번째 돌 역시 1열에서 떨어뜨린다고 되어 있다.

가다가 돌을 만났기 때문에, 우선 왼쪽 아래 칸으로 떨어져야 하는데, 조건을 보면 왼쪽 칸과 왼쪽 아래 칸 둘 다 빈 칸이어야 한다고 하였다. 그런데 빈 칸이고 뭐고 보드 바깥으로 넘어가기 때문에, 왼쪽으로는 갈 수 없다. 따라서, 오른쪽으로 가야 한다. 오른쪽 칸, 오른쪽 아래 칸 둘 다 비었으므로, 오른쪽 아래 칸으로 이동한다.
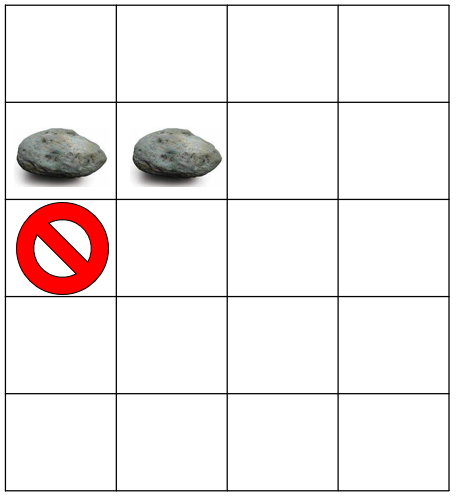
그럼 열이 1열에서 2열로 바뀌었다. 그런데 2열에는 아무것도 없다. 그럼 맨 끝까지 떨어져야 하는데, 이것을 위해서 우리는 R+1행 전부 벽이 존재한다고 가정할 것이다.
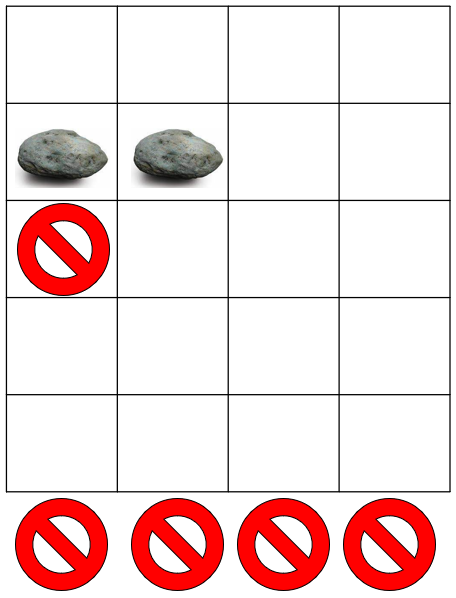
물론 실제로 벽이 있다는 것은 아니지만 벽이 있다고 생각하는 것이 마음 편하다. 아무튼 두번째 돌은 떨어지다가 R행에서 벽을 만나기 때문에, (R, 2)로 떨어진다.
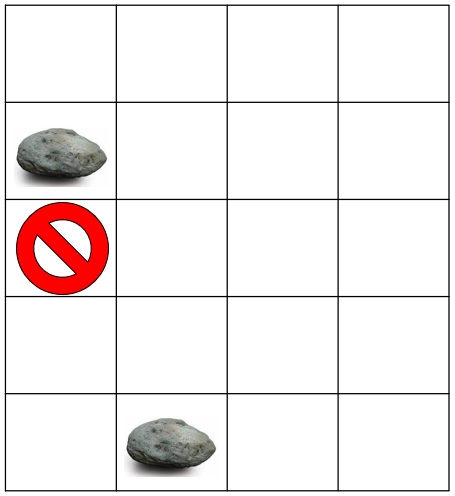
그런데, 조건을 보아하니, 한 번 완전히 떨어진 돌은 다시는 움직이지 않는 것 같다. 따라서 1열의 돌도 움직이지 않을 것이다. 그럼 다음에 1열에서 떨어뜨릴 돌들은 반드시 (2, 1)에 있는 돌과 부딪힐 것이다. 이렇게 알고 있는 정보를 활용하지 않고 일일히 돌이 떨어지는 경로를 구한다면, 앞서 말했던 것처럼 시간이 오래 걸릴 것이다. 따라서, Col열에서 돌이 부딪힐 곳을 미리 저장해 두고, 돌이 떨어진다면 그 정보를 사용해서 경로를 구한다면, 굳이 일일히 경로를 찾을 필요가 없어질 것이다.
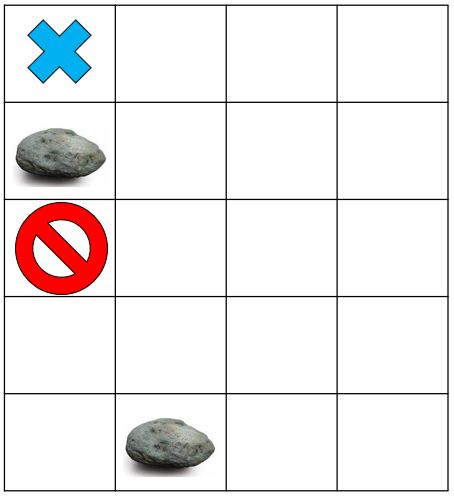
돌이 부딪힐 체크포인트를 담을 변수는 stack 배열로 선언하였으며, 스택에는 돌이 부딪히는 좌표를 순서쌍으로 저장하였다.
이제 세 번째 돌을 떨어뜨릴 건데, 이번에도 1열에서 떨어뜨릴 것이다.
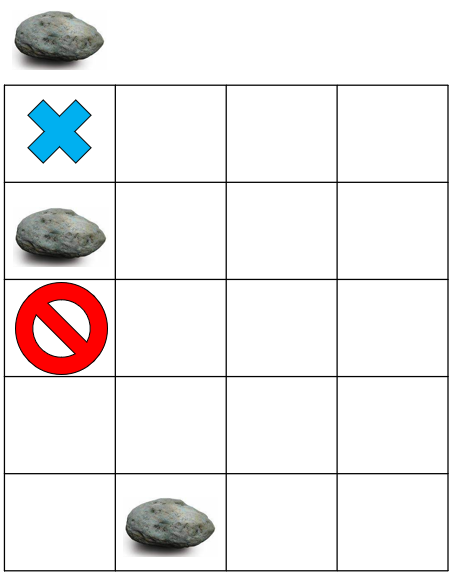
그런데 이미 두번째 돌이 부딪히면서 남기고 간 체크포인트가 존재한다. 그리고 그 체크포인트는 현재 빈칸이다. 따라서, 세번째 돌은 (1, 1)에서 떨어지기 시작한다. 역시나 왼쪽은 보드 밖이므로, 오른쪽으로 떨어진다. 그리고 (4, 2)에서 두번째 돌과 부딪힌다. 부딪히면서 왼쪽을 살펴보니, (4, 1), (5, 1) 둘 다 비어 있는 상태이다. 따라서 왼쪽 아래 칸인 (5, 1)로 떨어진다. 그리고 두번째 돌과 부딪혔기 때문에, (4, 2)를 1번째 스택에 push한다. 1번째인 이유는 원래 1열에서 떨어뜨리는 돌이었기 때문이다.
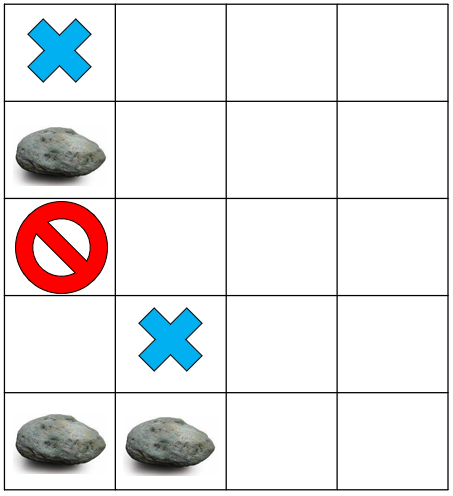
이렇게 되면, 다음에 또 1열에서 돌을 떨어뜨린다면, 저 두 체크포인트를 이용할 수 있고(엄밀히 말하면 1번째 스택의 top인 (4, 2)가 비어 있기 때문에 저 체크포인트로 떨어지고, 또한 top을 제외한 나머지 원소들 역시 비어 있다는 것이 자명하기 때문에) 그럼 당연히 (4, 2)에서 시작할 것이다.
그런데 놀랍게도 네번째 돌도 1열에서 떨어뜨린다.
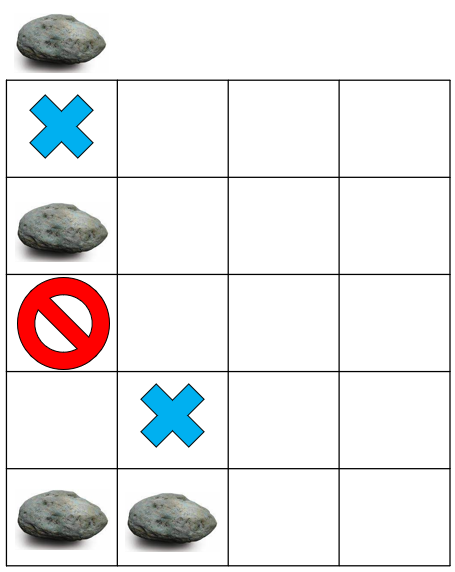
1열의 체크포인트를 확인해 보니, 스택의 top인 (4, 2)가 현재 비어 있다. 따라서 저기까지 이동할 수 있다. 따라서 (4, 2)부터 시작한다. 왼쪽을 확인해 보니, 왼쪽 아래 칸이 세 번째 돌로 막혀 있다. 따라서 저기로는 이동할 수 없다. 오른쪽 칸과 오른쪽 아래 칸은 비어 있다. 따라서 오른쪽 아래 칸으로 이동한다.
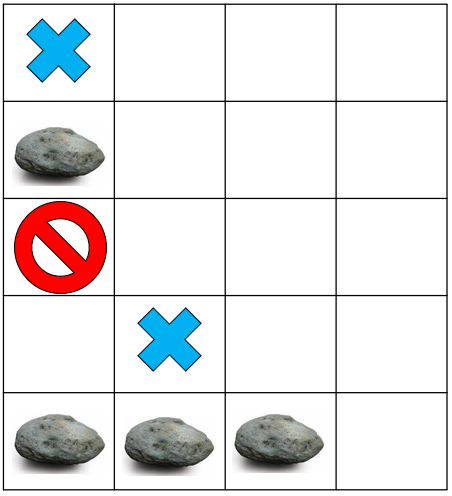
아까 말 안한 게 있는데, 세번째 돌이 (5, 1)로 떨어진 후, 계속 떨어져야 하나, 보드 바깥이라서 더 나갈 수가 없다. 하지만 아까 우리는 R+1행, 즉 6행 전부 벽으로 막혀 있다고 가정했다. 벽과 만났으므로, 그 자리에서 멈춰야 하고, 따라서 (5, 1)에서 멈춘 것이다. 네번째 돌도 마찬가지로 (5, 3)에서 멈췄다.
이렇게 예제 1을 통해서 구현 방법을 파악해보았다.
코드에서는 빈 칸을 0, 벽을 -1, 돌을 1로 표현했는데, 사실 안 그래도 되는데 왜 그랬는지는 모르겠다. 데이터를 다 입력받았으면, 이제부터는 돌을 던져야 하는데, 돌을 던지기 전에 돌을 던질 열 Col번째 스택에 push되어 있는 체크포인트 정보를 확인한다.

Col번째 스택의 top 좌표 (Y, X)에 해당하는 칸이 비었다면, 돌은 (1, Col)이 아닌 (Y, X)부터 시작한다. 아까도 말했지만, top 좌표가 비었다면, 당연히 다른 원소들에 해당하는 칸들도 비었다는 뜻이다. 마지막으로 Col열에서 던진 돌이 이전 체크포인트들을 다 거치고 나서 top에 해당하는 좌표를 체크포인트로 찍었다는 뜻이므로. 하지만 top좌표에 해당하는 칸이 빈 칸이 아니라면, 해당 체크포인트에 돌이 더 이상 갈 수가 없으므로 제거한다(pop). 이렇게 남은 체크포인트들이 전부 비어 있지 않아 전부 사용할 수 없다면, 원래대로 (1, Col)에서 돌을 던진다.

돌이 떨어지는 과정은 재귀를 통하여 구현한다. 돌은 (Row, Col)에서부터 떨어지기 시작하고, 우선 비어 있지 않은, 해당 열에서 가장 높은 곳 H를 찾는다. 즉, (H, Col)은 벽이 있거나 돌이 있는 칸이다. (H, Col)에 벽이 있다면 더 이상 움직이지 않고 (H-1, Col)에 멈춰버린다. 하지만 (H, Col)에 돌이 있다면, 조건대로 우선 왼쪽 및 왼쪽 아래 칸부터 확인한다. 여기서 왼쪽 열이 보드 바깥이 아닌지 확인하는 예외처리 과정을 해준다. 둘 다 비어있다면, 현재 칸((H-1, Col))을 체크포인트로 지정하고 왼쪽 아래 칸((H-1, Col-1))으로 이동한 후 (H-1, Col-1)부터 다시 떨어지기 시작한다.(재귀) 왼쪽이 비어 있지 않다면 오른쪽을 확인하고, 오른쪽 역시 왼쪽과 마찬가지로 진행한다. 둘 다 막혀 있는 곳이 있다면, 돌은 그 자리에서 멈추게 된다. 이렇게 벽을 만나거나, 돌을 만났는데 왼쪽 오른쪽이 둘 다 막힐 때까지 재귀가 진행되며, 돌이 움직일 수 없는 상태가 되었다면 재귀는 끝나게 된다.
코드
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <unordered_map>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>
#define FIRST cin.tie(NULL); cout.tie(NULL); ios::sync_with_stdio(false);
#define MAX_R 30005
#define MAX_C 35
#define LL long long
#define INF 1e9
/*
직접적으로 돌의 경로를 찾아서 돌을 떨군다면 골드4~5정도의 난이도가 되겠지만
역시나 플래티넘 문제라 그런 어설픈 방법은 통하지 않는다.
왜냐하면 높이가 최대 3만까지인데, 돌까지 최대 10만번 던지니,
일반적인 방법으로 푼다면 시간 초과가 발생한다.
따라서 다른 방식으로 접근해야 한다.
구글링을 통해서 돌이 움직인 경로를 적어주는 방식으로 접근한다면,
다음 돌을 던질 때 돌이 어디로 갈 지 먼저 파악할 수 있으니,
시간을 많이 줄일 수 있다.
*/
using namespace std;
int R, C, N;
int MAP[MAX_R][MAX_C];
set<int> Wall[MAX_C]; // C열에 있는 장애물의 행
/*
각 열마다 존재하는 벽 또는 돌의 위치를 나타내기 위하여 set을 사용하였다.
set은 원소들을 자동으로 오름차순 정렬시켜주는 특징을 가지고 있다.
*/
stack<pair<int, int> > Check_Pos[MAX_C]; // 1행 C열에서 떨어뜨리는 돌의 체크포인트 좌표
/*
돌들의 경로를 저장해주기 위한 체크포인트이다.
체크포인트에 해당하는 칸의 바로 윗 칸에 돌이 떨어진다.
*/
void Stone_Falling(int Row, int Col, int First) { // Row, Col은 돌이 떨어지는 곳, First는 돌을 던졌던 처음 열
int H = *(Wall[Col].upper_bound(Row)); // Col열에서, 돌이 떨어지면서 다른 곳과 부딪힐 높이 찾기
if (MAP[H][Col] == 1) { // 떨어지는 돌이 H행 Col열에서 돌을 만났을 때
// 왼쪽 칸과 왼쪽 아래 칸이 빈 칸이라면 왼쪽 아래 칸으로 떨어진다. Col이 1 미만이 되면 안 되므로 예외처리를 해준다.
if ((Col - 1 >= 1) && (MAP[H][Col - 1] == 0) && (MAP[H - 1][Col - 1] == 0)) {
// MAP[H - 1][Col - 1]가 바로 왼쪽 칸, MAP[H][Col - 1]이 바로 왼쪽 아래 칸을 의미한다.
Check_Pos[First].push(make_pair(H - 1, Col)); // 현재 돌이 왼쪽 아래 칸으로 떨어졌으므로, 체크포인트로 지정
Stone_Falling(H - 1, Col - 1, First); // 왼쪽 아래로 떨어진 후 다시 떨어질 체크포인트 찾기
}
// 오른쪽 칸과 오른쪽 아래 칸이 빈 칸이라면 오른쪽 아래 칸으로 떨어진다. Col이 C 초과가 되면 안 되므로 예외처리를 해준다.
else if ((Col + 1 <= C) && (MAP[H][Col + 1] == 0) && (MAP[H - 1][Col + 1] == 0)) {
Check_Pos[First].push(make_pair(H - 1, Col)); // 현재 돌이 오른쪽 아래 칸으로 떨어졌으므로, 체크포인트로 지정
Stone_Falling(H - 1, Col + 1, First); // 오른쪽 아래로 떨어진 후 다시 떨어질 체크포인트 찾기
}
// 떨어질 곳이 없다면 돌은 멈추고 다시는 움직이지 않는다.
else {
MAP[H - 1][Col] = 1;
Wall[Col].erase(H);
Wall[Col].insert(H - 1);
}
}
else { // 떨어지는 곳이 벽이라면
MAP[H - 1][Col] = 1; // 벽 위로 떨어진다.
Wall[Col].erase(H);
Wall[Col].insert(H - 1);
}
}
void Print() {
for (int i = 1; i <= R; i++) {
for (int j = 1; j <= C; j++) {
if (MAP[i][j] == 0) {
cout << ".";
}
else if (MAP[i][j] == 1) {
cout << "O";
}
else if (MAP[i][j] == -1) {
cout << "X";
}
}
cout << "\n";
}
}
int main() {
FIRST
cin >> R >> C;
for (int i = 1; i <= R; i++) {
string S;
cin >> S;
for (int j = 1; j <= C; j++) {
if (S[j - 1] == '.') {
MAP[i][j] = 0;
}
else if (S[j - 1] == 'X') {
MAP[i][j] = -1;
Wall[j].insert(i); // j열 i행에 벽이 생겼으므로, Wall[j]에 i를 insert한다.
}
}
}
for (int i = 1; i <= C; i++) {
// 행은 1부터 R까지 존재하므로, R+1행에 벽이 있다고 생각해도 상관없다.
Wall[i].insert(R + 1);
}
cin >> N;
for (int i = 0; i < N; i++) {
int Col, Y, X;
cin >> Col;
/*
돌을 떨어뜨릴 때, 이전 돌들이 이동한 경로를 찾아야 한다.
*/
while (!Check_Pos[Col].empty()) { // Col열에서의 현재 체크포인트
Y = Check_Pos[Col].top().first;
X = Check_Pos[Col].top().second;
if (MAP[Y][X] != 0) { // 현재 체크포인트가 빈 칸이 아닐 때, 즉 현재 체크포인트에 돌이 존재할 때
Check_Pos[Col].pop(); // 현재 칸에는 이제 돌이 존재하므로, 체크포인트로 사용될 수 없음
}
else { // 현재 체크포인트에 돌을 떨어뜨릴 것이다. 따라서 체크포인트를 더 탐색할 필요가 없으므로, 반복문을 종료한다.
break;
}
};
if (Check_Pos[Col].empty()) { // Col열에 체크포인트가 더 이상 없는 경우
Stone_Falling(1, Col, Col); // 이 때는 돌을 떨구기 위해 사용할 이전 돌들의 이동 경로가 없으므로, 처음 1행에서 돌을 떨군다.
}
else { // Col열에 체크포인트가 존재하는 경우
Stone_Falling(Y, X, Col); // 이 때는 이미 돌을 1행에서 떨구어, 돌이 (Y, X)까지 왔을 때이므로, 시작점을 (Y, X)로 한다.
}
}
Print();
return 0;
}
출처
돌 그림 : https://wikis.krsocsci.org/index.php?title=%EA%B3%B5%ED%95%AD%ED%9D%AC%EB%A7%9D%EB%8F%8C
'BOJ > Platinum ~ Diamond' 카테고리의 다른 글
| [BOJ/Platinum 5] 백준 19235 모노미노도미노(C++) (0) | 2022.01.27 |
|---|---|
| [BOJ/Platinum 5] 백준 2642 전개도(C++) (0) | 2022.01.26 |
| [BOJ/Platinum 5] 백준 19541 역학 조사(C++) (0) | 2022.01.25 |
| [BOJ/Platinum 5] 백준 17470 배열 돌리기 5(C++) (0) | 2022.01.24 |
| [BOJ/Platinum 5] 백준 5373 큐빙(C++) (0) | 2022.01.23 |
