[BOJ/Platinum 5] 백준 17470 배열 돌리기 5(C++)

문제 링크

https://www.acmicpc.net/problem/17470

17470번: 배열 돌리기 5

크기가 N×M인 배열이 있을 때, 배열에 연산을 R번 적용하려고 한다. 연산은 총 6가지가 있다. 1번 연산은 배열을 상하 반전시키는 연산이다. 1 6 2 9 8 4 → 4 2 9 3 1 8 7 2 6 9 8 2 → 9 2 3 6 1 5 1 8 3 4 2 9 →

www.acmicpc.net

문제

크기가 N×M인 배열이 있을 때, 배열에 연산을 R번 적용하려고 한다. 연산은 총 6가지가 있다.

1번 연산은 배열을 상하 반전시키는 연산이다.

1 6 2 9 8 4 → 4 2 9 3 1 8
7 2 6 9 8 2 → 9 2 3 6 1 5
1 8 3 4 2 9 → 7 4 6 2 3 1
7 4 6 2 3 1 → 1 8 3 4 2 9
9 2 3 6 1 5 → 7 2 6 9 8 2
4 2 9 3 1 8 → 1 6 2 9 8 4
  <배열>      <연산 결과>

2번 연산은 배열을 좌우 반전시키는 연산이다.

1 6 2 9 8 4 → 4 8 9 2 6 1
7 2 6 9 8 2 → 2 8 9 6 2 7
1 8 3 4 2 9 → 9 2 4 3 8 1
7 4 6 2 3 1 → 1 3 2 6 4 7
9 2 3 6 1 5 → 5 1 6 3 2 9
4 2 9 3 1 8 → 8 1 3 9 2 4
  <배열>      <연산 결과>

3번 연산은 오른쪽으로 90도 회전시키는 연산이다.

1 6 2 9 8 4 → 4 9 7 1 7 1
7 2 6 9 8 2 → 2 2 4 8 2 6
1 8 3 4 2 9 → 9 3 6 3 6 2
7 4 6 2 3 1 → 3 6 2 4 9 9
9 2 3 6 1 5 → 1 1 3 2 8 8
4 2 9 3 1 8 → 8 5 1 9 2 4
  <배열>      <연산 결과>

4번 연산은 왼쪽으로 90도 회전시키는 연산이다.

1 6 2 9 8 4 → 4 2 9 1 5 8
7 2 6 9 8 2 → 8 8 2 3 1 1
1 8 3 4 2 9 → 9 9 4 2 6 3
7 4 6 2 3 1 → 2 6 3 6 3 9
9 2 3 6 1 5 → 6 2 8 4 2 2
4 2 9 3 1 8 → 1 7 1 7 9 4
  <배열>      <연산 결과>

5, 6번 연산을 수행하려면 배열을 크기가 N/2×M/2인 4개의 부분 배열로 나눠야 한다. 아래 그림은 크기가 6×8인 배열을 4개의 그룹으로 나눈 것이고, 1부터 4까지의 수로 나타냈다.

1 1 1 1 2 2 2 2
1 1 1 1 2 2 2 2
1 1 1 1 2 2 2 2
4 4 4 4 3 3 3 3
4 4 4 4 3 3 3 3
4 4 4 4 3 3 3 3

5번 연산은 1번 그룹의 부분 배열을 2번 그룹 위치로, 2번을 3번으로, 3번을 4번으로, 4번을 1번으로 이동시키는 연산이다.

3 2 6 3 1 2 9 7 → 2 1 3 8 3 2 6 3
9 7 8 2 1 4 5 3 → 1 3 2 8 9 7 8 2
5 9 2 1 9 6 1 8 → 4 5 1 9 5 9 2 1
2 1 3 8 6 3 9 2 → 6 3 9 2 1 2 9 7
1 3 2 8 7 9 2 1 → 7 9 2 1 1 4 5 3
4 5 1 9 8 2 1 3 → 8 2 1 3 9 6 1 8
    <배열>          <연산 결과>

6번 연산은 1번 그룹의 부분 배열을 4번 그룹 위치로, 4번을 3번으로, 3번을 2번으로, 2번을 1번으로 이동시키는 연산이다.

3 2 6 3 1 2 9 7 → 1 2 9 7 6 3 9 2
9 7 8 2 1 4 5 3 → 1 4 5 3 7 9 2 1
5 9 2 1 9 6 1 8 → 9 6 1 8 8 2 1 3
2 1 3 8 6 3 9 2 → 3 2 6 3 2 1 3 8
1 3 2 8 7 9 2 1 → 9 7 8 2 1 3 2 8
4 5 1 9 8 2 1 3 → 5 9 2 1 4 5 1 9
    <배열>           <연산 결과>

입력

첫째 줄에 배열의 크기 N, M과 수행해야 하는 연산의 수 R이 주어진다.

둘째 줄부터 N개의 줄에 배열 A의 원소 Aij가 주어진다.

마지막 줄에는 수행해야 하는 연산이 주어진다. 연산은 공백으로 구분되어져 있고, 문제에서 설명한 연산 번호이며, 순서대로 적용시켜야 한다.

출력

입력으로 주어진 배열에 R개의 연산을 순서대로 수행한 결과를 출력한다.

제한

2 ≤ N, M ≤ 100
1 ≤ R ≤ 2,000,000
N, M은 짝수
1 ≤ Aij ≤ 108

예제 입력 1

6 8 1
3 2 6 3 1 2 9 7
9 7 8 2 1 4 5 3
5 9 2 1 9 6 1 8
2 1 3 8 6 3 9 2
1 3 2 8 7 9 2 1
4 5 1 9 8 2 1 3
1

예제 출력 1

4 5 1 9 8 2 1 3
1 3 2 8 7 9 2 1
2 1 3 8 6 3 9 2
5 9 2 1 9 6 1 8
9 7 8 2 1 4 5 3
3 2 6 3 1 2 9 7

예제 입력 2

6 8 1
3 2 6 3 1 2 9 7
9 7 8 2 1 4 5 3
5 9 2 1 9 6 1 8
2 1 3 8 6 3 9 2
1 3 2 8 7 9 2 1
4 5 1 9 8 2 1 3
2

예제 출력 2

7 9 2 1 3 6 2 3
3 5 4 1 2 8 7 9
8 1 6 9 1 2 9 5
2 9 3 6 8 3 1 2
1 2 9 7 8 2 3 1
3 1 2 8 9 1 5 4

예제 입력 3

6 8 1
3 2 6 3 1 2 9 7
9 7 8 2 1 4 5 3
5 9 2 1 9 6 1 8
2 1 3 8 6 3 9 2
1 3 2 8 7 9 2 1
4 5 1 9 8 2 1 3
3

예제 출력 3

4 1 2 5 9 3
5 3 1 9 7 2
1 2 3 2 8 6
9 8 8 1 2 3
8 7 6 9 1 1
2 9 3 6 4 2
1 2 9 1 5 9
3 1 2 8 3 7

예제 입력 4

6 8 1
3 2 6 3 1 2 9 7
9 7 8 2 1 4 5 3
5 9 2 1 9 6 1 8
2 1 3 8 6 3 9 2
1 3 2 8 7 9 2 1
4 5 1 9 8 2 1 3
4

예제 출력 4

7 3 8 2 1 3
9 5 1 9 2 1
2 4 6 3 9 2
1 1 9 6 7 8
3 2 1 8 8 9
6 8 2 3 2 1
2 7 9 1 3 5
3 9 5 2 1 4

예제 입력 5

6 8 1
3 2 6 3 1 2 9 7
9 7 8 2 1 4 5 3
5 9 2 1 9 6 1 8
2 1 3 8 6 3 9 2
1 3 2 8 7 9 2 1
4 5 1 9 8 2 1 3
5

예제 출력 5

2 1 3 8 3 2 6 3
1 3 2 8 9 7 8 2
4 5 1 9 5 9 2 1
6 3 9 2 1 2 9 7
7 9 2 1 1 4 5 3
8 2 1 3 9 6 1 8

예제 입력 6

6 8 1
3 2 6 3 1 2 9 7
9 7 8 2 1 4 5 3
5 9 2 1 9 6 1 8
2 1 3 8 6 3 9 2
1 3 2 8 7 9 2 1
4 5 1 9 8 2 1 3
6

예제 출력 6

1 2 9 7 6 3 9 2
1 4 5 3 7 9 2 1
9 6 1 8 8 2 1 3
3 2 6 3 2 1 3 8
9 7 8 2 1 3 2 8
5 9 2 1 4 5 1 9

예제 입력 7

6 8 6
3 2 6 3 1 2 9 7
9 7 8 2 1 4 5 3
5 9 2 1 9 6 1 8
2 1 3 8 6 3 9 2
1 3 2 8 7 9 2 1
4 5 1 9 8 2 1 3
1 2 3 4 5 6

예제 출력 7

3 1 2 8 9 1 5 4
1 2 9 7 8 2 3 1
2 9 3 6 8 3 1 2
8 1 6 9 1 2 9 5
3 5 4 1 2 8 7 9
7 9 2 1 3 6 2 3

알고리즘 분류

구현

풀이

지금까지의 배열 돌리기 문제를 생각하고 접근하면 큰코다치는 문제였다.

본인은 돌리다가 하도 안돼서, 이 형님의 글을 읽어보고 느낌을 잡았다.

우선 최악의 경우를 생각해보자. 100*100의 배열에 200만번의 연산을 해주는 것이다.

이걸 그냥 돌려주면 시간 초과가 날 것이다. 돌리는 과정에서 배열을 복사하고 회전시키고 다시 복사하고..

따라서, 배열을 압축해준다면, 시간이 초과되지 않을 것이다.

5, 6번 연산을 보면, 배열을 4개의 그룹으로 나눈다고 하였다. 4개의 그룹으로 나누기 때문에 행과 열의 길이는 무조건 짝수로 되어있는 것을 볼 수 있다.

따라서, 우리는 배열을 4개의 그룹으로 나눌 것이다. 그리고 그룹마다 존재하는 4개의 모서리, 그러니까 총 16개의 모서리만을 회전 연산에 이용할 것이다.

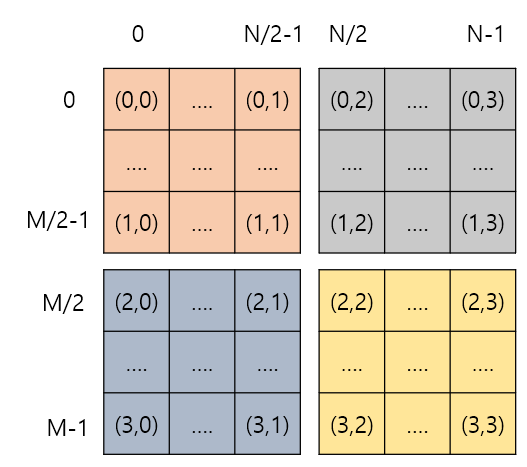
여기서 가능한 X좌표는 0, N/2-1, N/2, N-1, Y좌표는 0, M/2-1, M/2, M-1이 되며, 따라서 총 16가지의 좌표가 나올 수 있다. 정수와 정수를 한 쌍으로 하는 4*4 pair 배열을 선언해서 모서리의 좌표를 모두 담는다.

우리는 이 모서리의 정보들이 담긴 pair배열만을 이용해서 배열을 회전(시키는 척)해주면 되는 것이다.

1. 상하반전

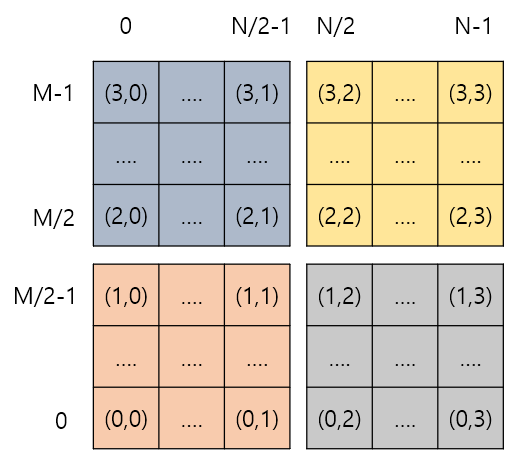
2. 좌우반전

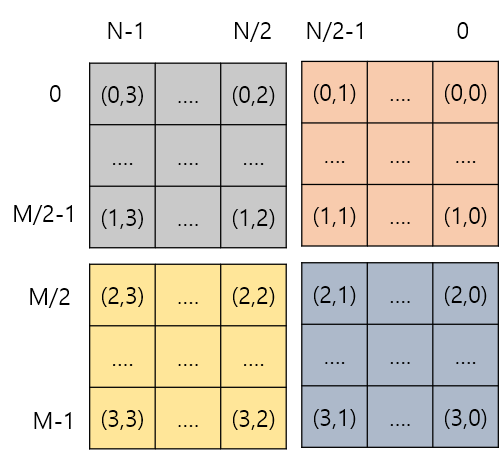
3. 오른쪽으로 90도 회전

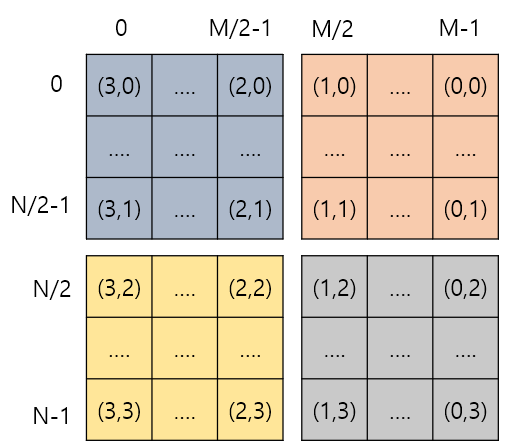
4. 왼쪽으로 90도 회전

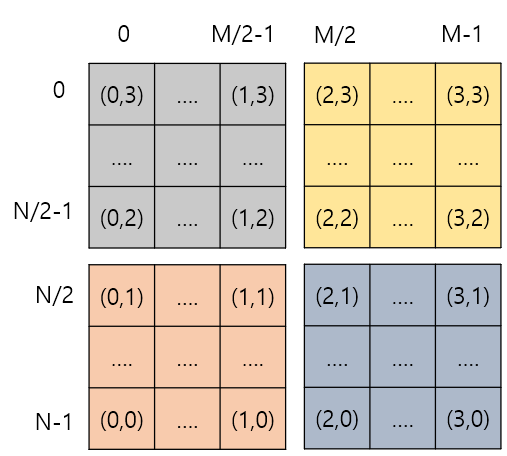
5. 4개의 배열 자체를 오른쪽으로 90도 회전

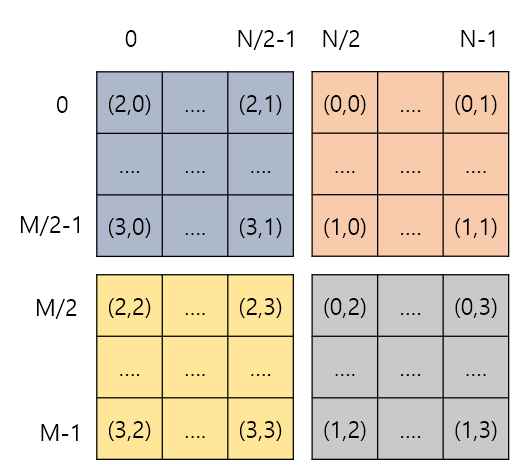
6. 4개의 배열 자체를 왼쪽으로 90도 회전

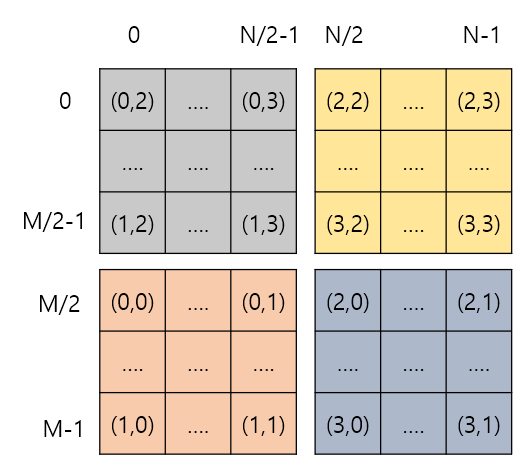
R번의 회전 연산을 모두 진행하는 것 자체는 어렵진 않았다. 왜냐하면 일반적인 배열 돌리기를 하면 문제 없기 때문이다.

이제 출력을 진행하면 되는데,

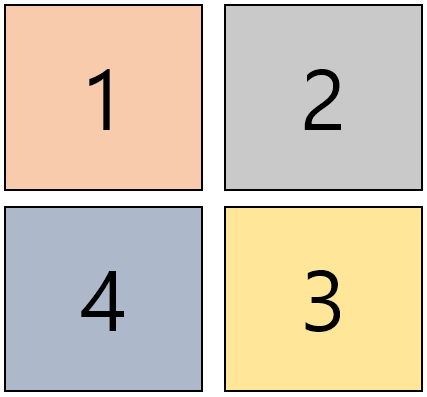
배열의 한 그룹에서 모서리가 이렇게 존재한다고 하면, 우리는 1번, 2번, 그리고 4번의 모서리들의 (X, Y)좌표를 비교해서 전체 배열 A의 해당 좌표에 있는 숫자를 출력하면 되는 것이다.

그런데 이대로만 구현해서 제출한다면 90%쯤에서 틀렸다고 나올 것이다. 왜 틀렸을까?

생각해보니 90% 언저리에서 틀린다면, 배열의 크기가 작거나, 아무튼 테스트케이스의 무언가가 아주 작은 경우에서 틀리는 것이라고 하였다.

배열 A의 행, 열의 길이가 둘 다 4 이상이라면, 정상적으로 작동한다. 왜냐하면, 4*4 배열이라도, 4그룹으로 나누면 한 그룹 당 2*2의 배열이며, 그룹당 4개의 모서리가 존재하기 때문이다.

하지만, 행이나 열 둘 중 하나의 길이가 2거나, 둘 다 2라면, 4그룹으로 나누었을 때 한 그룹당 모서리의 개수가 2개 이하로 나올 것이다. 그럼 코드가 정상적으로 작동하지 않을 것이다.

따라서, 행, 열의 길이가 둘 다 4 이상이 아닌 경우에는 그냥 배열을 직접 돌려주기로 하였다.

더 좋은 방법이 있겠지만, 본인은 백린이이기 때문에 이게 최선이었다.

더 좋은 방법이 있다면 제발 공유좀 부탁드린다.

코드

#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <unordered_map>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>
#define FIRST cin.tie(NULL); cout.tie(NULL); ios::sync_with_stdio(false);
#define MAX 105
#define LL long long
#define INF 1e9

using namespace std;
int N, M, R;
int ArrY[4];
int ArrX[4];
pair<int, int> MAP[4][4];
pair<int, int> Tmp[4][4];
int A[MAX][MAX];
int Tmp_A[MAX][MAX];
int answer[MAX][MAX];

/*
	최악의 경우의 수를 생각했을 때, 100X100 크기의 배열을 200만번 연산한다면
	시간 복잡도가 매우 커지게 된다. 따라서, 배열을 전체를 돌리는 것이 아닌,
	배열을 4등분했을 때 나오는 4개의 배열의 각각의 4개의 꼭짓점만 돌려준다.
	즉 핵심은 배열 4개로 나누고 배열별로 회전시키겠다는 것이다.
*/

void init() { // 배열 4개의 각각의 꼭짓점을 저장
	ArrY[0] = 0;
	ArrY[1] = (N / 2) - 1;
	ArrY[2] = (N / 2);
	ArrY[3] = N - 1;
	ArrX[0] = 0;
	ArrX[1] = (M / 2) - 1;
	ArrX[2] = (M / 2);
	ArrX[3] = M - 1;
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			MAP[i][j].first = ArrY[i];
			MAP[i][j].second = ArrX[j];
		}
	}
}

void Copy_MAP() {
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			Tmp[i][j] = MAP[i][j];
		}
	}
}

void First_Operation() { // 배열들의 각각의 모서리 부분만 상하반전
	Copy_MAP();
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			MAP[3 - i][j] = Tmp[i][j];
		}
	}
}

void Second_Operation() { // 배열들의 각각의 모서리 부분만 좌우반전
	Copy_MAP();
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			MAP[j][3 - i] = Tmp[j][i];
		}
	}
}

void Third_Operation() { // 배열들의 각각의 모서리 부분만 오른쪽으로 90도 회전
	Copy_MAP();
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			MAP[j][3 - i] = Tmp[i][j];
		}
	}
	swap(N, M);
}

void Fourth_Operation() { // 배열들의 각각의 모서리 부분만 왼쪽으로 90도 회전
	Copy_MAP();
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			MAP[3 - j][i] = Tmp[i][j];
		}
	}
	swap(N, M);
}

void Fifth_Operation() { // 4개의 배열 자체를 오른쪽으로 90도 회전
	pair<int, int> Tmp_MAP[2][2];
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			Tmp_MAP[i][j] = MAP[i][j];
		}
	}
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			MAP[i][j] = MAP[i + 2][j];
		}
	}
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			MAP[i + 2][j] = MAP[i + 2][j + 2];
		}
	}
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			MAP[i + 2][j + 2] = MAP[i][j + 2];
		}
	}
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			MAP[i][j + 2] = Tmp_MAP[i][j];
		}
	}
}

void Sixth_Operation() { // 4개의 배열 자체를 왼쪽으로 90도 회전
	pair<int, int> Tmp_MAP[2][2];
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			Tmp_MAP[i][j] = MAP[i][j];
		}
	}
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			MAP[i][j] = MAP[i][j + 2];
		}
	}
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			MAP[i][j + 2] = MAP[i + 2][j + 2];
		}
	}
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			MAP[i + 2][j + 2] = MAP[i + 2][j];
		}
	}
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			MAP[i + 2][j] = Tmp_MAP[i][j];
		}
	}
}

/*
	하지만 행의 길이나 열의 길이가 2라면, 배열을 4등분했을 때
	4개의 배열 각각의 모서리는 4개가 아니라 2개가 될 것이다.
	게다가, 2X2 배열이라면 모서리는 1개가 된다.
	따라서, 코드가 제대로 동작하지 않을 것이다.
	그래서 본인은 이러한 경우라면 그냥 배열 자체를 돌려주기로 했다.
	어차피 배열의 크기가 작기 때문에 시간 초과가 발생하지 않는다.
*/

void Copy_A() { // 배열 자체를 복사
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < M; j++) {
			Tmp_A[i][j] = A[i][j];
		}
	}
}

void First_Rotation() { // 배열 전체를 상하반전
	Copy_A();
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < M; j++) {
			A[(N - 1) - i][j] = Tmp_A[i][j];
		}
	}
}

void Second_Rotation() { // 배열 전체를 좌우반전
	Copy_A();
	for (int i = 0; i < M; i++) {
		for (int j = 0; j < N; j++) {
			A[j][(M - 1) - i] = Tmp_A[j][i];
		}
	}
}

void Third_Rotation() { // 배열 전체를 오른쪽으로 90도 회전
	Copy_A();
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < M; j++) {
			A[j][(N - 1) - i] = Tmp_A[i][j];
		}
	}
	swap(N, M);
}

void Fourth_Rotation() { // 배열 전체를 왼쪽으로 90도 회전
	Copy_A();
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < M; j++) {
			A[(M - 1) - j][i] = Tmp_A[i][j];
		}
	}
	swap(N, M);
}

void Fifth_Rotation() { // 나눈 4개의 배열 자체를 오른쪽으로 90도 회전
	for (int i = 0; i < (N / 2); i++) {
		for (int j = 0; j < (M / 2); j++) {
			Tmp_A[i][j] = A[i][j];
		}
	}
	for (int i = (N / 2); i < N; i++) {
		for (int j = 0; j < (M / 2); j++) {
			A[i - (N / 2)][j] = A[i][j];
		}
	}
	for (int i = (N / 2); i < N; i++) {
		for (int j = (M / 2); j < M; j++) {
			A[i][j - (M / 2)] = A[i][j];
		}
	}
	for (int i = 0; i < (N / 2); i++) {
		for (int j = (M / 2); j < M; j++) {
			A[i + (N / 2)][j] = A[i][j];
		}
	}
	for (int i = 0; i < (N / 2); i++) {
		for (int j = 0; j < (M / 2); j++) {
			A[i][j + (M / 2)] = Tmp_A[i][j];
		}
	}
}

void Sixth_Rotation() { // 나눈 4개의 배열 자체를 왼쪽으로 90도 회전
	for (int i = 0; i < (N / 2); i++) {
		for (int j = 0; j < (M / 2); j++) {
			Tmp_A[i][j] = A[i][j];
		}
	}
	for (int i = 0; i < (N / 2); i++) {
		for (int j = (M / 2); j < M; j++) {
			A[i][j - (M / 2)] = A[i][j];
		}
	}
	for (int i = (N / 2); i < N; i++) {
		for (int j = (M / 2); j < M; j++) {
			A[i - (N / 2)][j] = A[i][j];
		}
	}
	for (int i = (N / 2); i < N; i++) {
		for (int j = 0; j < (M / 2); j++) {
			A[i][j + (M / 2)] = A[i][j];
		}
	}
	for (int i = 0; i < (N / 2); i++) {
		for (int j = 0; j < (M / 2); j++) {
			A[i + (N / 2)][j] = Tmp_A[i][j];
		}
	}
}

/*
	배열들의 모서리만 회전시켰기 때문에 이제부터는 출력을 잘 해줘야 한다.
	4등분한 배열 각각을 따져봤을 때,
	첫 번째 꼭짓점의 X, Y좌표, 두 번째 꼭짓점의 X, Y좌표, 세 번째 꼭짓점의 X, Y좌표의 대소비교를 하여
	출력을 진행한다.
*/
void Arr_Copy(int startY, int startX, int endY, int endX, int FirstY, int FirstX) {
	int Y = FirstY;
	int X = FirstX;
	if ((MAP[startY][startX].first < MAP[endY][startX].first) && (MAP[startY][startX].second < MAP[startY][endX].second)) {
		for (int i = MAP[startY][startX].first; i <= MAP[endY][startX].first; i++) {
			for (int j = MAP[startY][startX].second; j <= MAP[startY][endX].second; j++) {
				answer[Y][X++] = A[i][j];
			}
			Y++;
			X = FirstX;
		}
	}
	else if ((MAP[startY][startX].first < MAP[endY][startX].first) && (MAP[startY][startX].second > MAP[startY][endX].second)) {
		for (int i = MAP[startY][startX].first; i <= MAP[endY][startX].first; i++) {
			for (int j = MAP[startY][startX].second; j >= MAP[startY][endX].second; j--) {
				answer[Y][X++] = A[i][j];
			}
			Y++;
			X = FirstX;
		}
	}
	else if ((MAP[startY][startX].first > MAP[endY][startX].first) && (MAP[startY][startX].second < MAP[startY][endX].second)) {
		for (int i = MAP[startY][startX].first; i >= MAP[endY][startX].first; i--) {
			for (int j = MAP[startY][startX].second; j <= MAP[startY][endX].second; j++) {
				answer[Y][X++] = A[i][j];
			}
			Y++;
			X = FirstX;
		}
	}
	else if ((MAP[startY][startX].first > MAP[endY][startX].first) && (MAP[startY][startX].second > MAP[startY][endX].second)) {
		for (int i = MAP[startY][startX].first; i >= MAP[endY][startX].first; i--) {
			for (int j = MAP[startY][startX].second; j >= MAP[startY][endX].second; j--) {
				answer[Y][X++] = A[i][j];
			}
			Y++;
			X = FirstX;
		}
	}
	else if ((MAP[startY][startX].first < MAP[startY][endX].first) && (MAP[startY][startX].second < MAP[endY][startX].second)) {
		for (int i = MAP[startY][startX].second; i <= MAP[endY][startX].second; i++) {
			for (int j = MAP[startY][startX].first; j <= MAP[startY][endX].first; j++) {
				answer[Y][X++] = A[j][i];
			}
			Y++;
			X = FirstX;
		}
	}
	else if ((MAP[startY][startX].first < MAP[startY][endX].first) && (MAP[startY][startX].second > MAP[endY][startX].second)) {
		for (int i = MAP[startY][startX].second; i >= MAP[endY][startX].second; i--) {
			for (int j = MAP[startY][startX].first; j <= MAP[startY][endX].first; j++) {
				answer[Y][X++] = A[j][i];
			}
			Y++;
			X = FirstX;
		}
	}
	else if ((MAP[startY][startX].first > MAP[startY][endX].first) && (MAP[startY][startX].second < MAP[endY][startX].second)) {
		for (int i = MAP[startY][startX].second; i <= MAP[endY][startX].second; i++) {
			for (int j = MAP[startY][startX].first; j >= MAP[startY][endX].first; j--) {
				answer[Y][X++] = A[j][i];
			}
			Y++;
			X = FirstX;
		}
	}
	else if ((MAP[startY][startX].first > MAP[startY][endX].first) && (MAP[startY][startX].second > MAP[endY][startX].second)) {
		for (int i = MAP[startY][startX].second; i >= MAP[endY][startX].second; i--) {
			for (int j = MAP[startY][startX].first; j >= MAP[startY][endX].first; j--) {
				answer[Y][X++] = A[j][i];
			}
			Y++;
			X = FirstX;
		}
	}
}

void Print() {
	Arr_Copy(0, 0, 1, 1, 0, 0);
	Arr_Copy(0, 2, 1, 3, 0, (M / 2));
	Arr_Copy(2, 0, 3, 1, (N / 2), 0);
	Arr_Copy(2, 2, 3, 3, (N / 2), (M / 2));
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < M; j++) {
			cout << answer[i][j] << " ";
		}
		cout << "\n";
	}
}

int main() {
	FIRST
	cin >> N >> M >> R;
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < M; j++) {
			cin >> A[i][j];
		}
	}
	if ((N >= 4) && (M >= 4)) { // 행과 열의 길이가 모두 4 이상일 때
		init();
		for (int i = 0; i < R; i++) {
			int X;
			cin >> X;
			if (X == 1) {
				First_Operation();
			}
			else if (X == 2) {
				Second_Operation();
			}
			else if (X == 3) {
				Third_Operation();
			}
			else if (X == 4) {
				Fourth_Operation();
			}
			else if (X == 5) {
				Fifth_Operation();
			}
			else if (X == 6) {
				Sixth_Operation();
			}
		}
		Print();
	}
	else { // 행 또는 열의 길이가 2, 혹은 둘 다 2일 때
		// 배열의 크기가 작기 때문에 그냥 배열 자체를 돌려줘도 시간 초과가 발생하지 않는다.
		for (int i = 0; i < R; i++) {
			int X;
			cin >> X;
			if (X == 1) {
				First_Rotation();
			}
			else if (X == 2) {
				Second_Rotation();
			}
			else if (X == 3) {
				Third_Rotation();
			}
			else if (X == 4) {
				Fourth_Rotation();
			}
			else if (X == 5) {
				Fifth_Rotation();
			}
			else if (X == 6) {
				Sixth_Rotation();
			}
		}
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < M; j++) {
				cout << A[i][j] << " ";
			}
			cout << "\n";
		}
	}
    
	return 0;
}

'BOJ > Platinum ~ Diamond' 카테고리의 다른 글

[BOJ/Platinum 5] 백준 2642 전개도(C++) (0)	2022.01.26
[BOJ/Platinum 4] 백준 3025 돌 던지기(C++) (0)	2022.01.26
[BOJ/Platinum 5] 백준 19541 역학 조사(C++) (0)	2022.01.25
[BOJ/Platinum 5] 백준 5373 큐빙(C++) (0)	2022.01.23
[BOJ/Platinum 5] 백준 23289 온풍기 안녕!(C++) (0)	2022.01.21

문제 링크

문제

입력

출력

제한

예제 입력 1

예제 출력 1

예제 입력 2

예제 출력 2

예제 입력 3

예제 출력 3

예제 입력 4

예제 출력 4

예제 입력 5

예제 출력 5

예제 입력 6

예제 출력 6

예제 입력 7

예제 출력 7

알고리즘 분류

풀이

코드

'BOJ > Platinum ~ Diamond' 카테고리의 다른 글

티스토리툴바