17822번: 원판 돌리기
반지름이 1, 2, ..., N인 원판이 크기가 작아지는 순으로 바닥에 놓여있고, 원판의 중심은 모두 같다. 원판의 반지름이 i이면, 그 원판을 i번째 원판이라고 한다. 각각의 원판에는 M개의 정수가 적혀
www.acmicpc.net
문제
반지름이 1, 2, ..., N인 원판이 크기가 작아지는 순으로 바닥에 놓여있고, 원판의 중심은 모두 같다. 원판의 반지름이 i이면, 그 원판을 i번째 원판이라고 한다. 각각의 원판에는 M개의 정수가 적혀있고, i번째 원판에 적힌 j번째 수의 위치는 (i, j)로 표현한다. 수의 위치는 다음을 만족한다.
- (i, 1)은 (i, 2), (i, M)과 인접하다.
- (i, M)은 (i, M-1), (i, 1)과 인접하다.
- (i, j)는 (i, j-1), (i, j+1)과 인접하다. (2 ≤ j ≤ M-1)
- (1, j)는 (2, j)와 인접하다.
- (N, j)는 (N-1, j)와 인접하다.
- (i, j)는 (i-1, j), (i+1, j)와 인접하다. (2 ≤ i ≤ N-1)
아래 그림은 N = 3, M = 4인 경우이다.

원판의 회전은 독립적으로 이루어진다. 2번 원판을 회전했을 때, 나머지 원판은 회전하지 않는다. 원판을 회전시킬 때는 수의 위치를 기준으로 하며, 회전시킨 후의 수의 위치는 회전시키기 전과 일치해야 한다.
다음 그림은 원판을 회전시킨 예시이다.
 |
 |
 |
| 1번 원판을 시계 방향으로 1칸 회전 | 2, 3번 원판을 반시계 방향으로 3칸 회전 | 1, 3번 원판을 시계 방향으로 2칸 회전 |
원판을 아래와 같은 방법으로 총 T번 회전시키려고 한다. 원판의 회전 방법은 미리 정해져 있고, i번째 회전할때 사용하는 변수는 xi, di, ki이다.
- 번호가 xi의 배수인 원판을 di방향으로 ki칸 회전시킨다. di가 0인 경우는 시계 방향, 1인 경우는 반시계 방향이다.
- 원판에 수가 남아 있으면, 인접하면서 수가 같은 것을 모두 찾는다.
- 그러한 수가 있는 경우에는 원판에서 인접하면서 같은 수를 모두 지운다.
- 없는 경우에는 원판에 적힌 수의 평균을 구하고, 평균보다 큰 수에서 1을 빼고, 작은 수에는 1을 더한다.
원판을 T번 회전시킨 후 원판에 적힌 수의 합을 구해보자.
입력
첫째 줄에 N, M, T이 주어진다.
둘째 줄부터 N개의 줄에 원판에 적힌 수가 주어진다. i번째 줄의 j번째 수는 (i, j)에 적힌 수를 의미한다.
다음 T개의 줄에 xi, di, ki가 주어진다.
출력
원판을 T번 회전시킨 후 원판에 적힌 수의 합을 출력한다.
제한
- 2 ≤ N, M ≤ 50
- 1 ≤ T ≤ 50
- 1 ≤ 원판에 적힌 수 ≤ 1,000
- 2 ≤ xi ≤ N
- 0 ≤ di ≤ 1
- 1 ≤ ki < M
예제 입력 1
4 4 1
1 1 2 3
5 2 4 2
3 1 3 5
2 1 3 2
2 0 1예제 출력 1
30원판의 초기 상태는 다음과 같다.

 |
 |
| x1 = 2, d1 = 0, k1 = 1 2번, 4번 원판을 시계 방향으로 1칸 돌린 후 |
인접하면서 수가 같은 것을 모두 지운 후 |
예제 입력 2
4 4 2
1 1 2 3
5 2 4 2
3 1 3 5
2 1 3 2
2 0 1
3 1 3예제 출력 2
22예제 1에서 이어진다.
 |
 |
| x2 = 3, d2 = 1, k2 = 3 3번 원판을 반시계 방향으로 3칸 돌린 후 |
인접하면서 수가 같은 것을 모두 지운 후 |
예제 입력 3
4 4 3
1 1 2 3
5 2 4 2
3 1 3 5
2 1 3 2
2 0 1
3 1 3
2 0 2예제 출력 3
22예제 2에서 이어진다.
 |
 |
| x3 = 2, d3 = 0, k3 = 2 2, 4번 원판을 시계 방향으로 2칸 돌린 후 |
인접하면서 수가 같은 것이 없다. 따라서, 평균 22/6 보다 작은 수는 +1, 큰 수는 -1 했다. |
예제 입력 4
4 4 4
1 1 2 3
5 2 4 2
3 1 3 5
2 1 3 2
2 0 1
3 1 3
2 0 2
3 1 1예제 출력 4
0예제 3에서 이어진다.
 |
 |
| x4 = 3, d4 = 1, k4 = 1 3번 원판을 반시계 방향으로 1칸 돌린 후 |
인접하면서 수가 같은 것을 모두 지운 후 |
예제 입력 5
4 6 3
1 2 3 4 5 6
2 3 4 5 6 7
3 4 5 6 7 8
4 5 6 7 8 9
2 1 4
3 0 1
2 1 2예제 출력 5
26알고리즘 분류
- 구현
- 시뮬레이션
풀이
원판을 회전시키는 방법만 생각한다면 어렵지 않은 문제였던 것 같다.
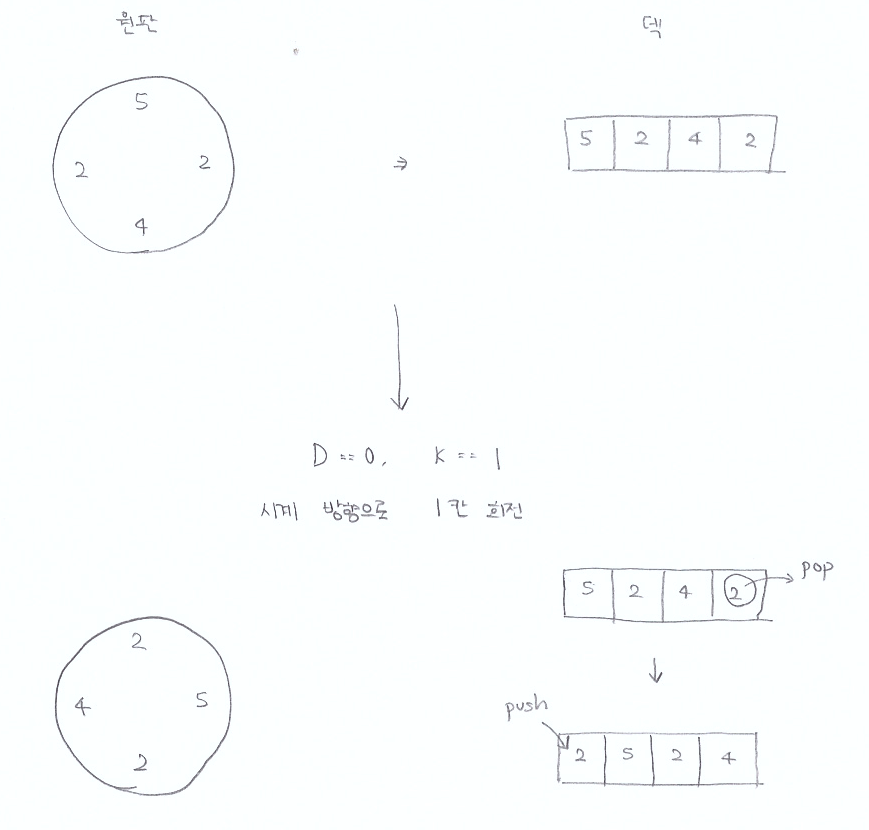
원판은 덱의 개념을 도입해서 회전시켰는데, 시계 방향 회전이라면 뒤의 K개의 숫자를 pop시킨 후 다시 front로 push하였고, 반시계 방향 회전이라면 앞의 K개의 숫자를 pop시킨 후 다시 back으로 push하였다. 복잡해질 것 같아서 실제로 덱을 사용하진 않았다. 대신 배열을 이용하여, tmp라는 배열을 새로 선언하여 여기에 복사한 후, 시계 방향 회전이라고 했을 때 tmp의 뒤의 K개의 숫자를 실제 원판 MAP의 앞에 놓고, 나머지 숫자는 원판의 뒤쪽에 놓는 식으로 하였다.
코드
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <unordered_map>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>
#define FIRST cin.tie(NULL); cout.tie(NULL); ios::sync_with_stdio(false);
#define MAX 55
#define INF 1e9
using namespace std;
int N, M, T;
int MAP[MAX][MAX];
bool Will_Erase[MAX][MAX];
void init() {
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
Will_Erase[i][j] = false;
}
}
}
void Rotation(int X, int D, int K) {
/*
원판 회전은 덱의 개념을 도입하여,
시계 방향으로 회전했을 때는 Back의 K개의 숫자가 pop되어서 다시 덱의 front로 push되고,
반시계 방향으로 회전했을 때는 front의 K개의 숫자가 pop되어서 다시 덱의 back으로 push되게 하였다.
물론 덱을 쓰면 복잡해질 것 같아서 덱을 쓰진 않았고 배열을 사용하였다.
*/
for (int i = X; i <= N; i += X) {
if (D == 0) {
int tmp[MAX];
for (int j = 1; j <= M; j++) {
tmp[j] = MAP[i][j];
}
for (int j = 1; j <= (M - K); j++) {
MAP[i][j + K] = tmp[j];
}
for (int j = (M - K + 1); j <= M; j++) {
MAP[i][j - (M - K)] = tmp[j];
}
}
else if (D == 1) {
int tmp[MAX];
for (int j = 1; j <= M; j++) {
tmp[j] = MAP[i][j];
}
for (int j = 1; j <= K; j++) {
MAP[i][j + (M - K)] = tmp[j];
}
for (int j = K + 1; j <= M; j++) {
MAP[i][j - K] = tmp[j];
}
}
}
}
void Erase_Number() {
init();
bool Same_Number = false; // 같은 숫자가 있어 숫자가 지워졌다면 true로 초기화
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
if (MAP[i][j] == 0) {
continue;
}
int Left = j - 1;
int Right = j + 1;
int Top = i + 1;
int Bottom = i - 1;
if (Left == 0) { // j가 1이라면 왼쪽의 숫자는 M번째 숫자가 될 것이다.
Left = M;
}
if (Right == M + 1) { // j가 M이라면 오른쪽의 숫자는 1번째 숫자가 될 것이다.
Right = 1;
}
bool Flag = false; // 같은 숫자가 하나라도 존재한다면 true로 초기화
if (MAP[i][j] == MAP[i][Left]) {
Flag = true;
Will_Erase[i][Left] = true; // 지울 숫자를 마킹
}
if (MAP[i][j] == MAP[i][Right]) {
Flag = true;
Will_Erase[i][Right] = true;
}
if (MAP[i][j] == MAP[Top][j]) {
if (i < N) {
Flag = true;
Will_Erase[Top][j] = true;
}
}
if (MAP[i][j] == MAP[Bottom][j]) {
if (i > 1) {
Flag = true;
Will_Erase[Bottom][j] = true;
}
}
if (Flag) {
Will_Erase[i][j] = true;
Same_Number = true;
}
}
}
if (Same_Number) {
// 같은 숫자가 존재한다면 마킹한 숫자들을 지운다.
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
if (Will_Erase[i][j]) {
MAP[i][j] = 0;
}
}
}
}
else { // 같은 숫자가 존재하지 않는다면
int sum = 0;
int size = 0;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
if (MAP[i][j] > 0) {
sum += MAP[i][j];
size++;
}
}
}
// 평균을 구한다. 이 평균보다 높은 숫자는 -1, 낮은 숫자는 +1한다.
double avg = (double)sum / (double)size;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
if (MAP[i][j] > 0) {
if (avg > (double)MAP[i][j]) {
MAP[i][j]++;
}
else if (avg < (double)MAP[i][j]) {
MAP[i][j]--;
}
}
}
}
}
}
int Calc_Sum() {
// 원판에 남아 있는 모든 숫자들을 더한다.
int res = 0;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
res += MAP[i][j];
}
}
return res;
}
int main() {
FIRST
cin >> N >> M >> T;
// 원판의 처음 상태 설정
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
cin >> MAP[i][j];
}
}
for (int i = 0; i < T; i++) {
int X, D, K;
cin >> X >> D >> K;
// 원판 회전
Rotation(X, D, K);
// 지울 수 있는 숫자 지우기
Erase_Number();
}
cout << Calc_Sum() << "\n"; // 남아 있는 숫자들의 합
return 0;
}'BOJ > Gold' 카테고리의 다른 글
| [BOJ/Gold 3] 백준 20327 배열 돌리기 6(C++) (0) | 2022.01.14 |
|---|---|
| [BOJ/Gold 3] 백준 18808 스티커 붙이기(C++) (0) | 2022.01.13 |
| [BOJ/Gold 3] 백준 16986 인싸들의 가위바위보(C++) (0) | 2022.01.12 |
| [BOJ/Gold 3] 백준 14676 영우는 사기꾼?(C++) (0) | 2022.01.12 |
| [BOJ/Gold 3] 백준 13168 내일로 여행(C++) (0) | 2022.01.12 |
